АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Дифференциал ф-ции и его геометрический смысл. Св-ва дифференциала

Читайте также:
  1. VI Дифференциальные уравнения
  2. Анализ резисторной дифференциальной системы
  3. Анализ трансформаторной дифференциальной системы
  4. Аналоговые перемножители на дифференциальных каскадах
  5. Бланк методики «Культурно-ценностный дифференциал» 1 страница
  6. Бланк методики «Культурно-ценностный дифференциал» 10 страница
  7. Бланк методики «Культурно-ценностный дифференциал» 11 страница
  8. Бланк методики «Культурно-ценностный дифференциал» 12 страница
  9. Бланк методики «Культурно-ценностный дифференциал» 13 страница
  10. Бланк методики «Культурно-ценностный дифференциал» 14 страница
  11. Бланк методики «Культурно-ценностный дифференциал» 2 страница
  12. Бланк методики «Культурно-ценностный дифференциал» 3 страница

limy=A, y=A+a

limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx

Dx®0

Dy=y`Dx+e, где e-б.м.в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.

dy=y`Dx

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.

Если y=x, то dy=dx=x`Dx=Dx, dx=Dx

Если y¹x, то dy=y`dx, y`=dy,dx

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x0,f(x0)) при изменении x0 на величину Dx

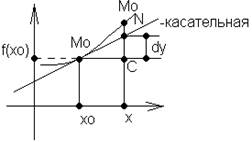
Дифференциал функции - это произведение производной f ’(x 0) и приращения аргумента :

df = f ’(x 0) · .

Для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на .

Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами.

 


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)