Проверка адекватности регрессивной модели и значимость показателей тесноты связи

Для характеристики среднего разброса относительно линии регрессии вполне подходит остаточная сумма квад­ратов. Неудобство состоит в том, чтоона зависит от чис­ла коэффициентов в уравнении: введите столько коэф­фициентов, сколько вы провели независимых опытов, и получите остаточную сумму, равную нулю. Поэтому предпочитают относить ее на один «свободный» опыт. Число таких опытов называется числом степеней свобо­ды f. Числом степеней свободы в статистике называется разность между числом опытов и числом коэффициентов (констант), которые уже вычислены по результатам этих опытов независимо друг от друга.

Остаточная сумма квадратов, деленная на число сте­пеней свободы, называется остаточной диспер­сией, или дисперсией адекватности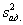

.

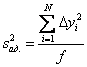В статистике разработан критерий, который очень удобен для проверки гипотезы об адекватности модели. Он называется F -критерием Фишера и определяется сле­дующей формулой:

.

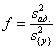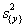– это дисперсия воспроизводимости со своим числом степеней свободы.

Удобство использования критерия Фишера состоит в том, что проверку гипотезы можно свести к сравнению с табличным значением. Если рассчитанное значение F -критерия не превы­шает табличного, то, с соответствующей доверительной вероятностью, модель можно считать адекватной. При превышении табличного значения эту приятную гипотезу приходится отвергать.

Показатели тесноты связей. При изучении корреляционной связи важным направлением анализа является оценка степени тесноты связи. Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой. При статистическом изучении взаимосвязей, как правило, учитываются только основные факторы. А вопрос необходимо ли вообще изучать более подробно данную связь и практически ее использовать, решается с учетом степени тесноты связи. Зная количественную оценку тесноты корреляционной связи, таким образом, можно решить следующую группу вопросов: 1) необходимо ли глубокое изучение данной связи между признаками и целесообразно ли ее практическое применение; 2) сопоставляя оценки тесноты связи для различных условий, можно судить о степени различий в ее проявлении в конкретных условиях; 3) последовательное рассмотрение и сравнение признака у с различными факторами (х1, х21, …) позволяет выявить, какие из этих факторов в данных конкретных условиях являются главными, решающими факторами, а какие второстепенными, незначительными факторами; Показатели тесноты связи должны удовлетворять ряду основных требований: 1) величина показателя степени тесноты связи должна быть равна или близка к нулю, если связь между изучаемыми признаками (процессами, явлениями) отсутствует; 2) при наличии между изучаемыми признаками (х и у) функциональной связи величина степень тесноты связи равна единице; 3) при наличии между признаками (х и у) корреляционной связи показатель тесноты связи выражается правильной дробью, которая по величине тем больше, чем теснее связь между изучаемыми признаками (стремится к единице); 4) при прямолинейной корреляционной связи показатели тесноты связи отражают и направление связи: знак (+) означает наличие прямой (положительной) связи; а знак (-) – обратной (отрицательной). Для характеристики степени тесноты корреляционной связи могут применяться различные статистические показатели: коэффициент Фехнера (КФ), коэффициент линейной (парной) корреляции (r’), коэффициент детерминации, корреляционное отношение (), индекс корреляции, коэффициент множественной корреляции (R), коэффициент частной корреляции (r’) и др. В данном вопросе рассмотрим коэффициент линейной корреляции (r) и корреляционное отношение. Более совершенным статистических показателем степени тесноты корреляционной связи является линейный коэффициент корреляции (r). При расчете коэффициента корреляции сопоставляются абсолютные значения отклонений индивидуальных величин факториального признака х и результативного признака у от их средних. Однако непосредственно сопоставлять между собой эти полученные результаты нельзя, т.к. признаки, как правило, выражены в различных единицах и даже при наличии одинаковых единиц измерения будут иметь различные по величине средние и различные вариации. В этой связи сравнению подлежат отклонения, выраженные в относительных величинах, т.е. в долях среднего квадратического отклонения (их называют нормированными отклонениями).

28. Общее понятие индексов в статистике, их свойства. Индексы - относительные показатели, предназначенные для описания изменения величины какого-либо явления во времени, пространстве или по сравнению с любым эталоном. Индексы мо­гут использоваться не только для сопоставления уровней явле­ний, но и для установления значимости причин, вызывающих их изменение. Основной элемент индексного соотношения - индексируе­мая величина, которая представляет собой значение признака статистической совокупности, изменение которой является объ­ектом изучения. С помощью индексов решаются следующие основные задачи: 1) характеризуется общее изменение сложных социально­-экономических явлений и отдельных его элементов (изучается развитие национальной экономики в целом и ее отдельных отрас­лей, определяется уровень жизни населения и т.д.); 2) выясняется роль отдельных факторов в формировании важнейших экономических показателей; 3) являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией - сравнение в пространстве, а также с планами, нормативами, про­гнозами и т. д.; 4) используются в международных сопоставлениях макроэкономических показателей, то есть производится пересчет зна­чений показателей из фактических цен в сопоставимые.

29. Виды индексов. Индивидуальные индексы. Важное значение в статистических исследованиях коммерческой деятельности имеет индексный метод. Полученные на основе этого метода показатели используются для характеристики развития анализируемых показателей во времени, по территории, изучения структуры и взаимосвязей, выявления роли факторов в изменении сложных явлений. Индекс – это относительная величина, показывающая во сколько раз уровень изучаемого явления в данных условиях, отличается от уровня того же явления в других условиях. Статистический индекс — это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию. Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость и достигается единство. Виды индексов различают по следующим факторам: по степени охвата элементов совокупности: индивидуальные – характеризуют изменение только одного элемента совокупности; сводные (общие) – отражают изменения по всей совокупности элементов сложного явления. Их разновидностью являются групповые индексы. в зависимости от содержания и характера индексируемой величины: индексы количественных показателей (например, индекс физического объема); индексы качественных показателей (например, индекс цен, себестоимости, производительности труда). в зависимости от методологии расчета: агрегатные – могут быть рассчитаны как индексы переменного и постоянного состава; средние из индивидуальных – получаются путем нахождения общих индексов с использованием индивидуальных.

Индивидуальные индексы характеризуют изменения отдельных единиц статистической совокупности. Различают следующие индивидуальные индексы: - индекс физического объема – показывает во сколько раз увеличился (уменьшился) объем в натуральных единицах в отчетном периоде по сравнению с базисным; - индекс цен – показывает во сколько раз увеличилась (уменьшилась) цена единицы продукции в отчетном периоде по сравнению с базисным; - индекс себестоимости – показывает во сколько раз увеличилась (уменьшилась) себестоимость единицы продукции в отчетном периоде по сравнению с базисным. Но если необходимо определить общее изменение объема производства или продаж, когда выпускаются различные виды продукции, рассчитывают общие индексы. Индекс становится общим, когда в расчетной формуле показывается неоднородность изучаемой совокупности. Он может быть рассчитан как агрегатный и как средний из индивидуальных. Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность и обладают следующими свойствами: - синтетические – посредством индексного метода производится соединение (агрегирование) в целом разнородных единиц статистической совокупности; - аналитические – посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. Примером неоднородной совокупности является общая масса проданных товаров нескольких видов. Тогда сумма выручки может быть записана в виде агрегата – это сумма произведений взвешивающего показателя на объемный.

Поиск по сайту: