 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МЕТОДЫ ОПИТИЗАЦИИ
1. Нормированное линейное пространство. Утверждения о квадрате нормы суммы. Выпуклые множества.
2. Теорема о существовании и единственности проекции точки на выпуклое замкнутое множество.
3. Критерий проекции 
точки 
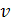на выпуклое множество (
).
4. Первая теорема отделимости (о существовании гиперплоскости, проходящей через внешнюю относительно 
точку 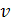, где 
-- выпуклое множество).
5. Теорема о существовании производной выпуклой функции по любому направлению в любой внутренней точке выпуклого множества.
6. Лемма – критерий выпуклости дифференцируемой функции (
).
7. Выпуклость множеств с вогнутыми ограничениями.
8. Необходимое условие точки локального минимума на выпуклом множестве (
).
9. Теорема об оптимальности точки локального минимума выпуклой функции на выпуклом множестве. Выпуклость множества оптимальных точек.
10. Критерий оптимальной точки выпуклой и дифференцируемой функции 
на выпуклом множестве ().
11. Теорема о единственности оптимальной точки строго выпуклой функции на выпуклом множестве.
12. Свойство сильно выпуклой функции на выпуклом множестве
(
).
13. Свойство сильно выпуклой на функции о существовании и единственности оптимальной точки, когда выпукло и замкнуто.
14. Седловая точка 
функции Лагранжа как достаточное условие оптимальности точки 
.
15. Критерий оптимальной точки. (Теорема Куна-Таккера.)
16. Критерий седловой точки для дифференцируемой функции.
17. Критерий возможного направления для задачи выпуклого программирования с линейными ограничениями.
18. Критерий оптимальной точки задачи выпуклого программирования с линейными ограничениями.
19. Основная задача линейного программирования. Утверждение о двойственной задаче.
20. Теорема о единственности вариации.
21. Достаточное условие дифференцируемости функционала по Гато.
22. Необходимое условие экстремума функционала.
23. Основная лемма вариационного исчисления.
24. Формула для вариации.
25. Уравнение Эйлера, как необходимое условие точки экстремума из простейшей задачи вариационного исчисления.
26. Частные случаи простейшей задачи вариационного исчисления.
27. Экстремумы функционалов от вектор-функций.
28. Экстремумы функционалов, содержащих производные высших порядков.
29. Экстремумы функционалов, зависящих от функций двух переменных.
30. Постановка задачи оптимального управления. Принцип максимума Понтрягина.
Поиск по сайту: