Теоретическая часть. Для студентов технических специальностей

ОПТИКА

Для студентов технических специальностей

Цель работы: изучить явления дифракции света и определить длину световой волны с помощью дифракционной решетки.

Теоретическая часть

Дифракция - это явление, возникающее при распространении света в среде с резкими неоднородностями, которое заключается в огибании светом препятствий и прохождением его в область геометрической тени. Дифракция заключается в нарушении закона прямолинейного распространения света. Качественно дифракцию можно объяснить с помощью принципа Гюйгенса: любая точка в пространстве, до которой дошел фронт волны, становится точечным источником вторичных сферических волн. Огибающая этих волн дает положение волнового фронта в последующий момент времени. Важно помнить, что волновой фронт - это поверхность, и световые лучи перпендикулярны волновому фронту.

Пусть непрозрачный экран с отверстием освещается параллельным пучком лучей (рис.1).

Рис.1

Воспользовавшись принципом Гюйгенса, легко найти новое положение волнового фронта после прохождения света через отверстие и убедится в том, что световые лучи действительно отклоняются от первоначального прямолинейного распространения. Для того, чтобы описывать явление дифракции количественно, принцип Гюйгенса был дополнен Френелем. Дополнение Френеля касается источников вторичных волн: точечные источники вторичных сферических волн - когерентны и поэтому необходимо учитывать интерференцию этих волн при наложении (образование и min интенсивности).

Рассмотрим дифракцию в параллельных лучах на одной щели. Пусть параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана длинная узкая щель шириной АВ = а. Как только плоский фронт световой волны дойдет до щели, все ее точки станут точечными источниками когерентных волн и лучи от них будут распространяться во все стороны. Рассмотрим лучи, идущие под углом к первоначальному направлению (рис.2).

Рис.2

Если собрать их линзой на экране в точке Р, можно наблюдать результат их интерференции. Оптическая разность хода между двумя крайними лучами D = BC равна . Если угол таков, что D равно четному числу полуволн

()

тогда фронт световой волны (в пределах щели) разбивается на четное число 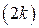плоских зон Френеля.

Плоские зоны Френеля обладают следующими свойствами: для любого луча, идущего от одной зоны, найдется соответственный луч, идущий от соседней зоны, так что разность хода между этими лучами равна и эти лучи взаимно гасят друг друга. Поэтому все световые волны от 2 соседних зон приходят в точку наблюдения в противофазе и гасят друг друга. Поэтому условие - есть условие min интенсивности в дифракционной картине. Если же , то поверхность фронта волны разбивается на нечетное число зон Френеля. Каждые две соседние зоны взаимно гасят друг друга, а действие одной из зон оказывается не компенсировано. Поэтому условие является условием max интенсивности для дифракции от одной щели. В направлении угла j = 0 лежит самый яркий max нулевого порядка, поскольку разность хода любых лучей, посылаемых щелью, в этом случае равна нулю. Поэтому лучи приходят в точку наблюдения в одной фазе, максимально усиливая друг друга.

При освещении щели монохроматическим светом на экране наблюдается дифракционная картина, состоящая из симметрично расположенных относительно центрального максимума нулевого порядка темных и светлых полос. Если щель освещается не монохроматическим светом, а белым, максимумы всех порядков, кроме нулевого, окрашены во все цвета радуги. Центральный же максимум - белый, т.к. при разность хода любых лучей, независимо от длины волны, равна нулю.

Для увеличения интенсивности и более четкого разделения цветов пользуются не одной щелью, а дифракционной решеткой (рис.3).

Рис.3

Она представляет собой ряд параллельных щелей одинаковой ширины (a), разделенных непрозрачными промежутками шириной (b). Суммарное расстояние a + b = d называется периодом или постоянной дифракционной решетки.

Пусть на N -щелевую решетку падает параллельный пучок монохроматического света (рис.4).

Рис.4

Согласно принципу Гюйгенса-Френеля все щели будут излучать вторичные когерентные волны. Расположив параллельно решетке линзу, в фокальной плоскости которой находится экран, можно наблюдать дифракционную картину. Для того, чтобы найти распределение интенсивности на экране, нужно учесть не только интерференцию волн, вышедших из каждой отдельной щели, но и интерференцию волн, пришедших в данную точку наблюдения P из соседних щелей.

Условие min интенсивности для одной щели является также условием главных max интенсивности и для дифракционной решетки. Действительно, если любая щель в отдельности не посылает света в направлениях, определяемых данным условием, действие всех щелей решетки в совокупности будет аналогичным. Если разность хода между лучами, идущими от двух соседних щелей, удовлетворяет условию , (m = 0, 1, 2,...), световые волны от всех щелей приходят в точку наблюдения P в одинаковых фазах, и взаимно усиливаясь, создают максимумы интенсивности дифракционной картины. Максимум, соответствующий 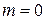, называется центральным, а максимумы при m = 1,2,3... называются max первого, второго, третьего порядков.

При освещении решетки не монохроматическим, а белым светом, световые полосы, соответствующие максимумам всех порядков, кроме нулевого, окрашены. С помощью дифракционной решетки с известным периодом можно определить длину световой волны , воспользовавшись условием max для малых углов:

где - расстояние от центрального максимума (m = 0) до максимума
- порядка; - расстояние от решетки до экрана.

Связь длины волны, частоты и энергии фотона приведена в инструкции А-12.

Поиск по сайту: