методические указания

для выполнения контрольной работы по дисциплине

«Эконометрика»

для студентов заочного отделения

специальности 060100 – Экономическая теория

Екатеринбург 2003

Методические указания для выполнения контрольной работы по дисциплине "Эконометрика" для студентов заочного отделения – Екатеринбург: Рос. гос. проф.-пед. ун-т, 2003. 18 с.

Составители: канд. физ.-мат. наук, доцент Чебыкин Л.С.

Рецензент: доктор физ.-мат. наук, профессор Бердышев Ю.И.

Одобрены на заседании кафедры высшей математики. Протокол № 7 от 26.03.2003 г.

Заведующий кафедрой Л.С. Чебыкин

Рекомендовано к печати методической комиссией машиностроительного факультета ИПИ РГППУ. Протокол № 8 от 14.04.2003 г.

Председатель методической комиссии

МСФ ИПИ РГППУ В.П. Подогов

© Российский государственный

профессионально-педагогический

университет, 2003

Введение

Данные методические указания предназначены в помощь студентам заочного обучения специальности 060100 (Экономическая теория) при самостоятельном выполнении контрольной работы по дисциплине «Эконометрика».

Содержание методических указаний разбито на 4 раздела, по числу задач в задании контрольной работы.

В каждом разделе рассматривается типовая задача по соответствующей теме. Дается развернутое решение типовой задачи, сопровождаемое исчерпывающими объяснениями. По ходу решения приводятся краткие теоретические сведения (методы, формулы, критерии), на которые опирается решение рассматриваемой задачи. В некоторых случаях делаются ссылки на рекомендуемую учебную литературу.

1. Парная линейная регрессия

Задача 1. Даны результаты 10-ти последовательных наблюдений над парой количественных переменных (X, Y):

Требуется:

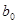1) Найти точечные статистические оценки и параметров и 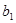линейной регрессии Y на X: .

2) На уровне значимости проверить гипотезу о согласии линейной регрессии с результатами наблюдений.

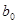3) С надежностью найти доверительные интервалы для параметров и 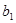линейной регрессии.

Решение:

1) Для уравнения прямой регрессии по статистическим данным найдем оценки и ее параметров методом наименьших квадратов. Применим известные ([1]) формулы

, ,

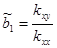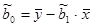где , ;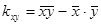

, , , .

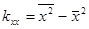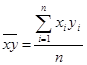Вычисления организуем в форме следующей расчетной таблицы:

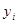
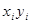
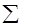
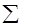n	83,3	78,5	7042,3	6280,7	6621,3

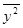
Далее вычисляем ковариации

;

;

;

и по указанным выше формулам находим

;

.

В результате получаем уравнение прямой регрессии

.

2) Проверим согласованность выбранной линейной регрессии с результатами наблюдений. Это выполняется как решение следующей задачи проверки статистической гипотезы.

На заданном уровне значимости выдвигается гипотеза об отсутствии линейной статистической связи. Для проверки выдвинутой гипотезы используется коэффициент детерминации 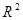и применяется статистика Фишера F ([1], [2], [3]).

В случае парной линейной регрессии коэффициент детерминации 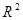равен квадрату выборочного коэффициента корреляции Пирсона, т.е.

.

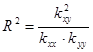Статистика F выражается формулой

.

и при условии справедливости гипотезы имеет классическое распределение Фишера с и степенями свободы.

В соответствии с приведенными формулами вычисляем коэффициент детерминации и наблюдаемое значение статистики Фишера:

;

.

Критическое значение статистики Фишера находим по таблице квантилей распределения Фишера ([4]), исходя из равенства

,

где (порядок квантили), . В данном случае .

Сравниваем между собой наблюдаемое и критическое значения статистики Фишера. Так как , то выдвинутая гипотеза 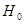решительно отвергается, что свидетельствует о согласии линейной регрессионной связи с результатами наблюдений.

3) Так как линейная регрессия согласуется со статистическими данными, найдем (с надежностью ) доверительные интервалы для параметров 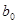и 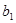линейной регрессии.

Применим известные формулы ([4]) для доверительных интервалов:

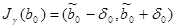; где

,

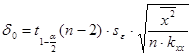- квантиль распределения Стьюдента порядка

с степенями свободы ([4]),

;

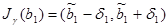, где

.

В данном случае ;

;

;

.

Применив приведенные выше формулы для доверительных интервалов, окончательно получим

;

;

следовательно,

;

.

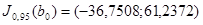2. трехмерная линейная регрессия

Задача 2. Даны результаты 11-ти последовательных наблюдений над тройкой количественных переменных (X₁, Х₂, Y):

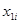
												(n=11)
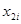
			-8	-10		-6		-12		-2	-4
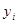
								-4		-3

Требуется:

1) Вычислить ковариации, составить ковариационную матрицу объясняющих переменных и вектор-столбец .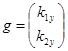

2) Найти статистические оценки параметров трехмерной линейной регрессии и составить уравнение плоскости регрессии .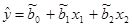

3) На уровне значимости проверить согласованность линейной трехмерной регрессионной модели с результатами наблюдений.

4) В случае согласованности с надежностью найти доверительные интервалы для параметров трехмерной линейной регрессии.

Решение:

1) Для вычисления ковариаций применим формулы

,

.

Вычисления средних величин, входящих в эти формулы, организуем в форме следующей расчетной таблицы:

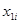
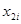
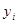
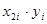
		-8					-72		-8
		-10					-110
		-6					-48		-18
		-12	-4				-120	-40
		-2	-3				-14	-21
		-4					-24		-20
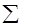
		-22					-376
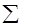n		-2				26,2727	-31,4545	7,7273	12,9091

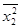
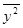
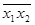
Затем последовательно вычисляем ковариации:

, ,

, ,

, .

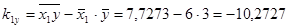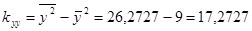Далее составим ковариантную матрицу объясняющих переменных и вектор-столбец .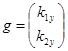

, .

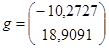2) Уравнение плоскости регрессии имеет вид 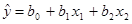. По статистическим данным найдем оценки параметров множественной линейной регрессии методом наименьших квадратов. Применим известную ([4], [5]) матричную формулу

,

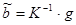где 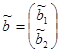; при этом .

Развернутые формулы принимают вид

, ,

.

По этим формулам находим

;

;

.

Таким образом, уравнение плоскости регрессии имеет вид

.

3) На уровне значимости проверим согласованность линейной трехмерной регрессионной модели со статистическими данными. Это выполняется как решение следующей задачи проверки статистической гипотезы. Выдвигается гипотеза 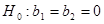об отсутствии линейной регрессионной связи. Для проверки выдвинутой гипотезы используется коэффициент детерминации 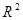и применяется статистика Фишера F ([1], [2], [4]).

В случае трехмерной линейной регрессии коэффициент детерминации и статистика Фишера выражается формулами

, .

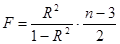При условии справедливости гипотезы 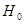случайная величина F имеет классическое распределение Фишера с 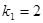и степенями свободы.

В соответствии с приведенными формулами вычисляем коэффициент детерминации 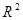и наблюдаемое значение статистики Фишера :

;

.

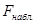Критическое значение статистики Фишера находим по таблице квантилей распределения Фишера ([4]), исходя из равенства

, где .

В рассматриваемом случае .

Так как, , то выдвинутая гипотеза 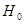решительно отвергается, что свидетельствует о согласии линейной трехмерной регрессии с результатами наблюдений.

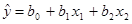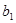4) Поскольку линейная множественная регрессия согласуется со статистическими данными, найдем (с надежностью ) доверительные интервалы для параметров и 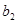плоскости регрессию

Применим известные формулы ([4]) для доверительных интервалов:

, ,

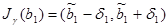где , ,

- квантиль распределения Стьюдента порядка с степенями свободы,

; - соответствующий диагональный элемент матрицы , т.е.

; .

В данном случае

;

;

; .

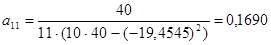Следовательно,

; .

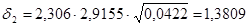Таким образом,

,

.

или окончательно

.

3. праболическая (квадратичная) регрессия

Задача 3. Даны результаты 7-и последовательных наблюдений над парой количественных показателей (X, Y):

	-3	-2	-1					(n=7)
	-10						-2

Требуется:

1) Построить диаграмму рассеяния и убедиться, что между переменными X и Y существует нелинейная связь.

2) Считая, что регрессия Y по X представляется многочленом 2-ой степени, найти статистические оценки параметров параболической регрессии и составить уравнение линии регрессии.

3) На уровне значимости проверить согласованность выбранной параболической регрессии с результатом наблюдений.

4) Если окажется, что параболическая регрессия согласуется со статистическими данными, то с надежностью найти доверительные интервалы для параметров этой регрессии.

Решение:

1) Строим диаграмму рассеяния, нанося на систему координат экспериментальные точки . y

● 5

● - 4 ●

- 3

- 2 ●

- 1

-3 -2 -1 0 1 2 3

- -1

- -2 ●

- -3

- -4

- -5

- -6

- -7

- -8

- -9

● - -10

По характеру расположения экспериментальных точек имеются все основания считать, что между переменными X и Y существует нелинейная статистическая связь.

2) Пусть уравнение линейной регрессии Y по X имеет вид

По статистическим данным задачи найдем MHK – оценки параметров параболической регрессии. Применение метода наименьших квадратов приводит к следующей системе нормальных уравнений ([1], [4]):

Разделим все уравнения на 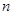и введем обозначения:

, , , ,

, , .

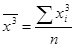Тогда система нормальных уравнений примет вид:

Из первого уравнения системы выразим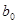

и подставим во 2-е и 3-е уравнения:

В результате для определения параметров 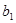и 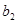получим следующую систему 2-х линейных уравнений:

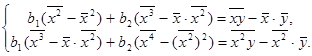
Для вычисления коэффициентов этой системы составим расчетную таблицу:

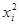
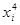
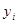
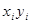
	-3		-27		-10			-90
	-2		-8
	-1		-1				-4
					-2		-6	-18
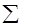
								-92
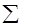n					0,4286	23,5714		-13,1429

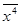
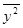
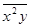
Отсюда находим

, , ,

, .

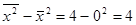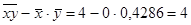Таким образом, система линейных уравнений имеет вид:

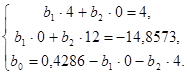
Решая полученную систему, находим статистические оценки параметров параболической регрессии:

, .

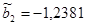Следовательно, уравнение линии регрессии Y по Х принимает вид:

.

3) На уровне значимости проверим согласованность выбранной параболической регрессии со статистическими данными. Это выполняется как решение задачи проверки статистической гипотезы. Выдвигается гипотеза об отсутствии параболической регрессионной связи. Для проверки этой гипотезы используется коэффициент детерминации 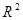и применяется статистика Фишера F.

В случае параболической регрессии формула для коэффициента детерминации может быть преобразована в виду ([4])

, где

, , .

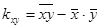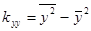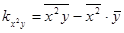Статистика F выражается формулой

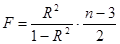
и при условии справедливости гипотезы 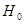имеет классическое распределение Фишера с 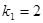и степенями свободы.

В соответствии с приведенными формулами последовательно вычисляем

, , ;

;

.

Критическое значение статистики Фишера находим по таблице квантилей распределения Фишера в соответствии с равенством:

, где .

В рассматриваемом случае .

Так как , то выдвинутая гипотеза 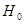решительно отвергается, что свидетельствует о согласии параболической регрессии с результатами наблюдений.

4) Поскольку параболическая (квадратичная) регрессия согласуется со статистическими данными, найдем (с надежностью ) доверительные интервалы для параметров этой регрессии.

Применим известные формулы ([4]) для доверительных интервалов:

;

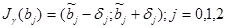где точность оценивания выражается равенством

;

здесь - квантиль распределения Стьюдента порядка с степенями свободы;

- исправленное среднее квадратическое отклонение остаточной компоненты («ошибки»);

- соответствующий диагональный элемент матрицы:

.

В данном случае

; ;

т.е. ; ; .

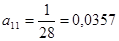Следовательно,

; ;

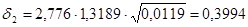; откуда находим

,

,

.

Таким образом, окончательно получаем

, ,

.

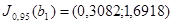4. прогнозировнаие на основе временного ряда

Задача 4. Дан временный ряд:

											(n=10)

Требуется:

1) Оценить параметры линейного тренда 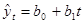методом наименьших квадратов.

2) На уровне значимости проверить согласованность линейной трендовой модели с результатами наблюдений.

3) На основании линейной трендовой модели определить точечный прогноз показателя Y на два шага вперед.

Решение:

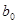1) По статистическим данным найдем статистические оценки и параметров и 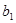линейного тренда 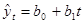методом наименьших квадратов. Для этого применим известные формулы:

, ,

где , ;

, , , .

Вычисления средних значений организуем в форме расчетной таблицы.

						; ; ;
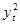
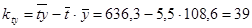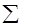
	5,5	108,6	38,5	12003,2	636,3

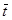
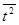
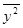
Таким образом, искомые оценки параметров линейного тренда равны , .

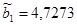Уравнение линейного тренда имеет вид

2) Проверка согласованности линейной трендовой модели со статистическими данными выполняется как решение задачи проверки статистической гипотезы об отсутствии линейной статистической связи на заданном уровне значимости . Для проверки гипотезы используется коэффициент детерминации и применяется статистика Фишера с и степени свободы.

В рассматриваемом случае ;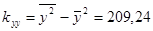

; .

Критическое значение статистики Фишера равно

.

Так как , то выдвинутая гипотеза 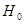отвергается, что свидетельствует о согласии линейной трендовой модели с результатами наблюдений.

3) По полученному уравнению линейного тренда найдем точечный прогноз показателя Y на два шага вперед ( - период упреждения). Для этого подставим в уравнение тренда значение времени (здесь n – длина данного временного ряда). Таким образом,

.

Рекомендуемая литература

1. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов /Под ред. Н.Ш.Кремера. – М.: ЮНИТИ-ДАНА, 2002. – 311 с.

2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс.– М.: Дело, 2000. – 400 с.

3. Эконометрика: Учебник /Под ред. И.И.Елисеевой.- М.: Финансы и статистика, 2001. – 344 с.

4. Сборник задач по математике для вузов. Специальные курсы /Под ред. А.В.Ефимова. – М.: Наука, 1984. – 608 с.

5. Ферстер Э., Ренц Б. Методы корреляционного и регрессионного анализа: Руководство для экономистов.- М.: Финансы и статистика, 1983. – 302 с.

Методические указания

для выполнения контрольной работы по дисциплине

«Эконометрика»

для студентов заочного отделения

Составитель: Чебыкин Л.С.

Подписано в печать __.__.2003. Формат 60х84/16. Бумага писчая № 1. Усл. печ. л. 1. Уч.-изд. л. 1. Тираж 2600 экз. Заказ № _ __.

Российский государственный профессионально-педагогический университет.

Екатеринбург, ул. Машиностроителей,11.

_______________________________________________________________________

Ротапринт РГППУ, ул. Каширская, 73.

Поиск по сайту: