 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
КОНТРОЛЬНАЯ РАБОТА. ЧАСТЬ 2
КОНТРОЛЬНАЯ РАБОТА. ЧАСТЬ 1.
Вариант 1
- Представить заданную функцию
 , где
, где  , в виде
, в виде  ; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке
; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке 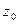
а)  ,
,  ,
,
b)  ,
, 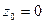
- Вычислить: а)
 , b)
, b) 
- Найти множество точек комплексной плоскости, заданных неравенством.
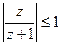
- Проверить является ли функция гармонической

- Восстановить аналитическую функцию
 , где
, где  , в виде
, в виде  по ее действительной части
по ее действительной части 
Вариант 2
- Представить заданную функцию
 , где
, где  , в виде
, в виде  ; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке
; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке 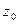
а)  ,
,  ,
,
b)  ,
, 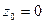
- Вычислить: а)
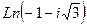 , b)
, b) 
- Найти множество точек комплексной плоскости, заданных неравенством.
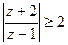
- Проверить является ли функция гармонической

- Восстановить аналитическую функцию
 , где
, где  , в виде
, в виде  по ее действительной части
по ее действительной части 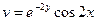
Вариант 3
- Представить заданную функцию
 , где
, где  , в виде
, в виде  ; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке
; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке 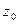
а)  ,
,  ,
,
b)  ,
, 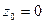
- Вычислить: а)
 , b)
, b) 
- Найти множество точек комплексной плоскости, заданных неравенством.
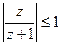
- Проверить является ли функция гармонической

- Восстановить аналитическую функцию
 , где
, где  , в виде
, в виде  по ее действительной части
по ее действительной части 
Вариант 4
- Представить заданную функцию
 , где
, где  , в виде
, в виде  ; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке
; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке 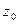
а)  ,
,  ,
,
b)  ,
, 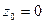
- Вычислить: а)
 , b)
, b) 
- Найти множество точек комплексной плоскости, заданных неравенством.
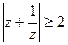
- Проверить является ли функция гармонической

- Восстановить аналитическую функцию
 , где
, где  , в виде
, в виде  по ее мнимой части
по ее мнимой части 
Вариант 5
- Представить заданную функцию
 , где
, где  , в виде
, в виде  ; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке
; проверить является ли она аналитической. Если да, то найти значение ее производной в заданной точке 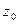
а) 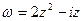 ,
,  ,
,
b)  ,
, 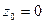
- Вычислить: а)
 , b)
, b) 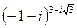
- Найти множество точек комплексной плоскости, заданных неравенством.
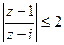
- Проверить является ли функция гармонической

- Восстановить аналитическую функцию
 , где
, где  , в виде
, в виде  по ее мнимой части
по ее мнимой части  ,
,  .
.
КОНТРОЛЬНАЯ РАБОТА. ЧАСТЬ 2.
Вариант 1
- Вычислить
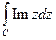 , где
, где  полуокружность
полуокружность 
- Разложить в ряд Лорана по степеням
 функцию
функцию  в области
в области 
- Определить характер особых точек для функций а)
 , b)
, b) 
- Найти вычеты функции а)
 , b)
, b) 
- Вычислите интеграл по замкнутому контуру
 , где
, где 
Вариант 2
- Вычислить
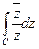 , где
, где 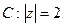 полуокружность
полуокружность 
- Разложить в ряд Лорана по степеням
 функцию
функцию  в области
в области 
- Определить характер особых точек для функций а)
 , b)
, b) 
- Найти вычеты функции а)
 , b)
, b) 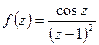
- Вычислите интеграл по замкнутому контуру
 , где
, где 
Вариант 3
- Вычислить
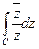 , где
, где  контур квадрата с вершинами в точках
контур квадрата с вершинами в точках  .
. - Разложить в ряд Лорана по степеням
 функцию
функцию  в области
в области 
- Определить характер особых точек для функций а)
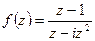 , b)
, b) 
- Найти вычеты функции а)
 , b)
, b) 
- Вычислите интеграл по замкнутому контуру
 , где
, где 
Вариант 4
- Вычислить
 , где
, где  ,
, 
- Разложить в ряд Лорана по степеням
 функцию
функцию  в области
в области 
- Определить характер особых точек для функций а)
 , b)
, b) 
- Найти вычеты функции а)
 , b)
, b) 
- Вычислите интеграл по замкнутому контуру
 , где
, где 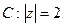
Вариант 5
- Вычислить
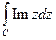 , где
, где  полуокружность
полуокружность 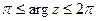
- Разложить в ряд Лорана по степеням
 функцию
функцию  в области
в области 
- Определить характер особых точек для функций а)
 , b)
, b) 
- Найти вычеты функции а)
 , b)
, b) 
- Вычислите интеграл по замкнутому контуру
 , где
, где 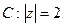
Поиск по сайту: