 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методические указания. Цель работы: овладение способами построения моделей линейной регрессии, выработка умения и навыков оценки надежности коэффициента корреляции
ПРАКТИЧЕСКАЯ РАБОТА № 2
ПОСТРОЕНИЕ МОДЕЛИ ЛИНЕЙНОЙ РЕГРЕССИИ
ПО ОПЫТНЫМ ДАННЫМ
Цель работы: овладение способами построения моделей линейной регрессии, выработка умения и навыков оценки надежности коэффициента корреляции, уравнения регрессии и его коэффициентов.
Содержание работы: на основании опытных данных требуется:
1. Построить корреляционное поле. По характеру расположения точек в корреляционном поле выбрать общий вид регрессии.
2. Вычислить числовые характеристики  ,
,  ,
, 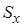 ,
, 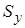 ,
,  ,
, 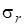 .
.
3. Определить значимость коэффициента корреляции  и найти для него доверительный интервал с надежностью
и найти для него доверительный интервал с надежностью  .
.
4. Написать эмпирические уравнения линий регрессий 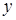 на
на  и
и  на
на 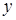 .
.
5. Вычислить коэффициент детерминации  и объяснить его смысловое значение.
и объяснить его смысловое значение.
6. Проверить адекватность уравнения регрессии 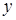 на
на  .
.
7. Провести оценку величины погрешности уравнения регрессии 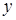 на
на  и его коэффициентов.
и его коэффициентов.
8. Построить уравнение регрессии 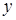 на
на  в первоначальной системе координат.
в первоначальной системе координат.
Разобранный пример.
В таблице №1 представлены результаты наблюдений зависимости средней заработной платы Y (тыс. руб.) от производительности труда X (тыс. руб.) по цеху технологической связи (по кварталам).
| Таблица № 1 | ||||||||||
| X | 24,3 | 24,9 | 28,1 | 30,5 | 31,5 | 39,3 | 40,2 | 43,5 | 45,4 | 45,9 |
| Y | 8,2 | 8,6 | 8,7 | 8,9 | 9,1 | 10,6 | 11,3 | 11,8 | 12,9 | 13,1 |
Методические указания
1) Построить на координатной плоскости точки 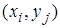 , пользуясь табл. №1. И около построенных точек провести линию тренда.
, пользуясь табл. №1. И около построенных точек провести линию тренда.
2) Вычислить статистики  ,
,  ,
, 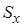 ,
, 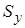 ,
,  .
.
Для вычисления статистик рекомендуется заполнить таблицу №2.
| Таблица №2 | |||||||

| 
| 
| 
| 
| 
| x 2 | 
|
| 24,3 | – 11,06 | 122,3236 | 8,2 | – 2,12 | 4,4944 | 590,49 | 199,26 |
| 24,9 | – 10,46 | 109,4116 | 8,6 | – 1,72 | 2,9584 | 620,01 | 214,14 |
| 28,1 | – 7,26 | 52,7076 | 8,7 | – 1,62 | 2,6244 | 789,61 | 244,47 |
| 30,5 | – 4,86 | 23,6196 | 8,9 | – 1,42 | 2,0164 | 930,25 | 271,45 |
| 31,5 | – 3,86 | 14,8996 | 9,1 | – 1,22 | 1,4884 | 992,25 | 286,65 |
| 39,3 | 3,94 | 15,5236 | 10,6 | 0,28 | 0,0784 | 1544,49 | 416,58 |
| 40,2 | 4,84 | 23,4256 | 11,3 | 0,98 | 0,9604 | 1616,04 | 454,26 |
| 43,5 | 8,14 | 66,2596 | 11,8 | 1,48 | 2,1904 | 1892,25 | 513,3 |
| 45,4 | 10,04 | 100,8016 | 12,9 | 2,58 | 6,6564 | 2061,16 | 585,66 |
| 45,9 | 10,54 | 11,0916 | 13,1 | 2,78 | 7,7284 | 2106,81 | 601,29 |
| 353,6 | 640,064 | 103,2 | 31,196 | 13143,36 | 3787,06 |
Тогда:
 — средняя производительность труда.
— средняя производительность труда.
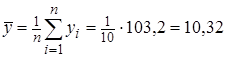 — средняя зарплата сотрудников цеха технологический связи,
— средняя зарплата сотрудников цеха технологический связи,
 Þ
Þ  ,
,
 Þ
Þ  ,
,
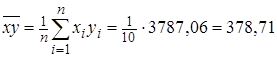 ,
,
 .
.
3) Для проверки значимости коэффициента корреляции необходимо вычислить статистику t p по формуле:
 .
.
По таблице критических точек распределения Стьюдента (уровень значимости  и числу степеней свободы
и числу степеней свободы 
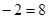 находим
находим  . Так как
. Так как  , выборочный коэффициент корреляции значимо отличается от нуля. То есть средняя зарплата Y и производительность X труда в цехе связаны линейной регрессионной зависимостью. Проводим приблизительную прямую с на числовой плоскости.
, выборочный коэффициент корреляции значимо отличается от нуля. То есть средняя зарплата Y и производительность X труда в цехе связаны линейной регрессионной зависимостью. Проводим приблизительную прямую с на числовой плоскости.
4) Находим доверительный интервал для выборочного коэффициента корреляции  с надежностью
с надежностью  .
.  .
.
 . Вычисляем среднюю квадратическую ошибку
. Вычисляем среднюю квадратическую ошибку 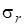 :
:
 .
.
Записываем доверительный интервал:
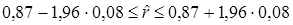
или  . Полученный результат означает, что по имеющейся выборке следует ожидать влияние производительности труда на рост средней зарплаты работников цеха технологической связи не менее чем на 71 %.
. Полученный результат означает, что по имеющейся выборке следует ожидать влияние производительности труда на рост средней зарплаты работников цеха технологической связи не менее чем на 71 %.
5) Найдем линейные уравнения регрессии 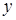 на
на  и
и  на
на 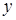 , которые являются приближенными уравнениями для истинных уравнений регрессий.
, которые являются приближенными уравнениями для истинных уравнений регрессий.
 |
Уравнение регрессии
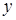 на
на  :
:
 Þ
Þ
 .
.
Уравнение регрессии  на
на 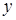 :
:
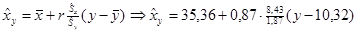 Þ
Þ
 .
.
Контроль вычислений:  ,
,
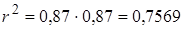 .
.
Так как условие  выполняется, то вычисления выполнены верно.
выполняется, то вычисления выполнены верно.
Из уравнения  следует, что при увеличении производительности труда на 1 тыс. руб. средняя зарплата работников цеха технологической связи возрастает на 192,989 рублей.
следует, что при увеличении производительности труда на 1 тыс. руб. средняя зарплата работников цеха технологической связи возрастает на 192,989 рублей.
6) Найдем точку пересечения линий регрессии. Подставляя  ,
,  в уравнения регрессий, получаем точки, координаты которых совпадают с координатами центра распределения
в уравнения регрессий, получаем точки, координаты которых совпадают с координатами центра распределения  .
.
7) Найдем коэффициент детерминации. Для линейной регрессии при вычисленном коэффициенте  он равен
он равен  . У нас
. У нас  . Это означает, что 76 % рассеивания средней зарплаты работников технологического цеха связи объясняется линейной регрессионной зависимостью между средней зарплатой и производительностью труда, и только 24 % рассеивания средней зарплаты работников технологического цеха остались необъяснимыми.
. Это означает, что 76 % рассеивания средней зарплаты работников технологического цеха связи объясняется линейной регрессионной зависимостью между средней зарплатой и производительностью труда, и только 24 % рассеивания средней зарплаты работников технологического цеха остались необъяснимыми.
8) Проверка адекватности уравнения линейной регрессии 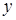 на
на  по критерию Фишера — Снедекора. Вычислим статистику
по критерию Фишера — Снедекора. Вычислим статистику  по формуле:
по формуле:
 , где
, где  .
.
Для нахождения суммы  составляем расчетную таблицу №3. Из табл. 2 и 3 находим:
составляем расчетную таблицу №3. Из табл. 2 и 3 находим:  ,
,  . Тогда
. Тогда
 ,
, 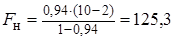 .
.
При уровне значимости  и числах степеней свободы
и числах степеней свободы 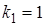 ,
,  по таблице критических точек распределения Фишера — Снедекора находим
по таблице критических точек распределения Фишера — Снедекора находим  . Так как
. Так как  , то заключаем, что уравнение линейной регрессии
, то заключаем, что уравнение линейной регрессии  статистически значимо описывает результаты эксперимента.
статистически значимо описывает результаты эксперимента.
9) Оценка величины погрешности уравнения регрессии  . Найдем относительную погрешность
. Найдем относительную погрешность  уравнения по формуле:
уравнения по формуле:
 ,
,
Где 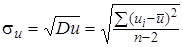 ,
,  ,
,  .
.
Так как  , то
, то 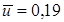 . Для нахождения суммы
. Для нахождения суммы  составляем табл. 4.
составляем табл. 4.
Тогда  ,
,  . Так как величина
. Так как величина  мала, то уравнение линейной регрессии
мала, то уравнение линейной регрессии  хорошо описывает опытные данные.
хорошо описывает опытные данные.
Оценим коэффициенты уравнения регрессии. У нас  ,
,  . Для нахождения отношений
. Для нахождения отношений 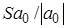 и
и  вычислим средние квадратические ошибки коэффициентов по формулам (68) и (69):
вычислим средние квадратические ошибки коэффициентов по формулам (68) и (69):
| Таблица 4 | ||

| 
| 
|
| 0,02 | – 0,17 | 0,0289 |
| 0,03 | – 0,16 | 0,0256 |
| – 0,2 | – 0,39 | 0,1521 |
| – 0,5 | – 0,69 | 0,4761 |
| – 0,5 | – 0,69 | 0,4761 |
| – 0,5 | – 0,69 | 0,4761 |
| 0,05 | – 0,14 | 0,0196 |
| – 0,1 | – 0,29 | 0,0841 |
| 0,7 | 0,51 | 0,2601 |
| 0,7 | 0,51 | 0,2601 |
| 2,2588 |
 ,
, 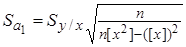 ,
,  .
.
По таблицам находим:  ,
,  . Учитывая, что
. Учитывая, что  ,
,  и
и  , находим:
, находим:
 ,
,
 ,
,
 .
.
Так как  и
и  , то коэффициенты
, то коэффициенты  и
и  уравнения регрессии
уравнения регрессии 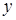 на
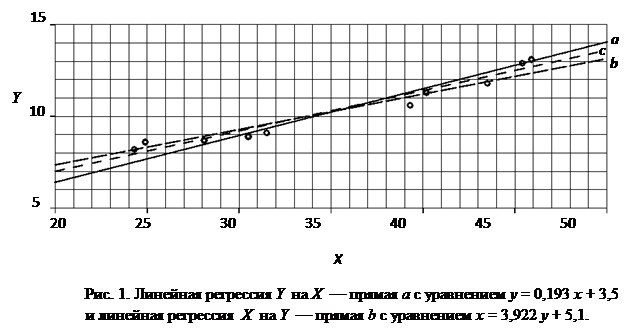
на  значимы. Графиками найденных регрессий являются прямые a, b, представленные на рис. 1.
значимы. Графиками найденных регрессий являются прямые a, b, представленные на рис. 1.
Вывод: Таким образом, уравнение регрессии  , описывающее зависимость средней зарплаты работников цеха технологической связи от производительности труда, значимо описывает опытные данные и может быть принято для практического руководства.
, описывающее зависимость средней зарплаты работников цеха технологической связи от производительности труда, значимо описывает опытные данные и может быть принято для практического руководства.
Варианты заданий для практической работы № 2 (ЦДО)
Номер варианта берется по двум последним цифрам зачетной книжки
Вариант № 1. Имеются данные, характеризующие зависимость между стоимостью X основных производственных фондов и объемом Y валовой продукции по десяти однотипным предприятиям:
| X | ||||||||||
| Y |
Вариант № 2. Зависимость между стоимостью X (тыс. млн. руб.) основных средств предприятий и месячным выпуском Y (тыс. руб.) продукции характеризуется следующими данными:
| X | |||||||
| Y |
Найти эмпирическую формулу функциональной зависимости месячного выпуска продукции от стоимости основных средств предприятий. Построить эмпирическую и теоретическую линии.
Вариант № 3. Имеются данные наблюдений изменения средней заработной платы Y (руб.) в зависимости от изменения производительности труда X (шт.) за 4 месяца 1992 года по девяти токарям цеха № 23 электромеханического завода:
| X | |||||||||
| Y | 518,5 | 813,5 | 1108,5 | 1403,5 | 1698,5 | 1993,5 | 2288,5 | 2583,5 | 2878,5 |
Вариант № 4. Дано распределение заводов по производственным средствам X (млн. руб.) и по суточной выработке Y (тыс. руб.):
| X | |||||||||||||||
| Y |
Вариант № 5. Данные нормы расхода моторного масла на угар и замену Y (л/100 л.т.) от максимальной мощности двигателя X (л.с.) приведены в таблице:
| X | 73,5 | |||||||||
| Y | 1,3 | 1,3 | 0,8 | 2,2 | 1,8 | 2,2 | 1,8 | 2,8 | 2,1 |
Вариант № 6. Результаты наблюдений изменения диаметра Y (мм) вала и износа X (мм) резца приведены в следующей таблице:
| X | 0,01 | 0,02 | 0,024 | 0,03 | 0,032 | 0,035 | 0,037 | 0,042 | 0,048 | 0,057 |
| Y | 20,01 | 20,014 | 20,022 | 20,024 | 20,027 | 20,029 | 20,034 | 20,04 | 20,049 |
Найти зависимость диаметра вала от износа резца.
Вариант № 7. Компанию по прокату автомобилей интересует зависимость между пробегом X автомобилей и стоимостью Y ежемесячного технического обслуживания. Для выяснения характера этой связи было отобрано 15 автомобилей. Данные приведены в таблице:
| X | |||||||||||||||
| Y |
Вариант № 8. При исследовании зависимости между выпуском готовой продукции Y (тыс. руб.)и энерговооруженностью труда X (кВт-час) получены следующие данные:
| X | ||||||||||||
| Y | 31,5 |
Вариант № 9. В таблице приведены данные, характеризующие зависимость израсходованных долот Y (шт.) при бурении 8 скважин в зависимости от механической скорости X (м/с) проходки:
| X | ||||||||||
| Y |
Вариант № 10. Скорость Y (м/час) бурения в твердых породах от нагрузки X (атм.) на долото характеризуется следующими данными:
| X | 10,5 | 11,5 | 12,5 | 13,5 | 13,8 | 15,5 | ||||
| Y | 3,5 | 2,5 | 2,5 | 1,5 | 0,5 | 0,5 | 1,2 | 3,5 |
Найти эмпирическую формулу зависимости Y от X.
Вариант № 11. Зависимость между выработкой продукции X (тыс. руб.) и затратами топлива Y в условных единицах характеризуется следующими данными:
| X | ||||||||||
| Y | 2,3 | 2,2 | 2,3 | 2,5 | 2,6 | 2,5 | 2,6 | 2,8 | 2,9 |
Вариант № 12. Имеются данные распределения заводов по производственным средствам X (млн. руб.) и по суточной выработке Y (млн. руб.):
| X | ||||||||||||
| Y |
Вариант № 13. Найти формулу, устанавливающую зависимость между коэффициентом Y сменности техники и ее средним возрастом Х по предприятию ПМК-7 объединения Сибкомплектмонтаж на основании следующих данных:
| Y | 1,18 | 1,21 | 1,25 | 1,26 | 1,3 | 1,32 | 1,33 | 0,69 | 0,72 | 0,8 |
| X | 6,31 | 5,8 | 5,1 | 5,6 | 6,1 | 6,5 | 6,55 | 3,8 | 3,41 |
Вариант № 14. Имеются данные о реализации продукции X (млн. руб.) и накладных расходах Y (тыс. руб.) на реализацию:
| X | ||||||||||
| Y |
Вариант № 15. Зависимость линейной нормы расхода топлива Y (л) от максимальной мощности двигателя автомобиля X (л.с.) характеризуется следующими данными:
| X | ||||||||||
| Y | 21,5 | 22,8 |
Вариант № 16. Имеются данные нормы расхода моторных масел на угар и замену Y (л/100 л.т.) в зависимости от максимального крутящего момента Х:
| X | 7,4 | 7,6 | 8,2 | 10,8 | ||||||
| Y | 1,3 | 1,3 | 1,5 | 1,8 | 2,2 | 2,1 | 2,8 | 2,6 | 2,3 | 2,4 |
Вариант № 17. Фазовая проницаемость нефти Y и насыщенность породы нефтью X характеризуются следующими данными:
| X | 0,05 | 0,15 | 0,25 | 0,35 | 0,45 | 0,55 | 0,65 | 0,75 | 0,85 | 0,95 |
| Y | 0,35 | 0,45 | 0,55 | 0,65 | 0,75 | 0,8 | 0,85 | 0,95 | 1,25 |
Вариант № 18. Имеются данные нормы расхода моторных масел на угар и замену Y (л/100 л.т.) в зависимости от максимальной мощности двигателя автомобиля X (л.с.):
| X | ||||||||||
| Y | 1,3 | 1,3 | 0,9 | 2,2 | 2,2 | 2,2 | 2,8 | 2,4 | 2,5 | 2,6 |
Вариант № 19. Зависимость между среднегодовой стоимостью основных производственных фондов X (млн. руб.) и стоимостью товарной продукции Y (млн. руб.) характеризуется следующими данными:
| X | 1,94 | 2,68 | 3,47 | 4,12 | 4,77 | 5,34 | 5,85 | 6,65 |
| Y | 0,82 | 0,97 | 1,06 | 1,08 | 1,1 | 1,14 | 1,21 | 1,25 |
Вариант № 20. Найти формулу, устанавливающую зависимость себестоимости одной тонны нефти Y (в руб.) от затрат X (в тыс. руб.) на одну тонну по следующим данным:
| X | 1,44 | 1,6 | 1,85 | 2,1 | 2,25 | 2,42 | 2,55 | 2,65 |
| Y | 161,5 |
Вариант № 21. Ниже приводятся данные о производительности труда Y (м) на одного чел/час и стаже рабочих X (в годах):
| X | ||||||||
| Y | 9,8 |
Вариант № 22. Найти формулу зависимости электрического сопротивления R (Ом) проводника от температурыQ˚С по следующим данным:
| Q | 19,1 | 25,0 | 30,1 | 36,0 | 40,0 | 45,1 | 50,0 |
| R | 76,30 | 77,80 | 79,75 | 80,80 | 82,35 | 83,90 | 85,10 |
Построить теоретическую и эмпирическую линии.
Вариант № 23. Найти зависимость израсходованных долот Y при бурении 10 скважин в зависимости от механической скорости X проходки на основании следующих данных:
| X | ||||||||||
| Y |
Вариант № 24. Имеются данные о реализованной продукции X (млн. руб.) и накладных расходах Y (тыс. руб.) на реализацию:
| X | ||||||||||
| Y |
Вариант № 25. В таблице приведены данные, характеризующие зависимость растворимости азотно-натриевой соли S в зависимости от температуры T:
| T | |||||||||
| S | 66,7 | 76,3 | 80,6 | 85,7 | 92,9 | 99,4 | 113,6 | 125,1 |
Вариант № 26. При исследовании зависимости хода Y (мм) поршня двигателя автомобиля от максимального крутящего момента X получены следующие данные:
| X | 7,4 | 8,2 | 10,8 | 18,4 | 47,5 | |||||
| Y |
Вариант № 27. Результаты исследования зависимости между средней месячной выработкой Y (млн. руб.) продукции на одного рабочего и стоимостью X (млн. руб.) основных производственных средствприведены в таблице:
| X | 9,9 | 10,0 | 10,1 | 10,2 | 10,3 | 10,4 | 10,5 | 10,6 |
| Y | 0,8 | 0,9 | 0,95 | 1,1 | 1,25 | 1,2 | 1,28 | 1,32 |
Вариант № 28. При исследовании зависимости между выработкой Y (тыс. руб.) и энерговооруженностью X (кВт / час) труда получены следующие данные:
| X | ||||||||||
| Y | 6,3 | 3,6 | 7,5 | 8,5 | 12,5 | 6,2 | 12,6 | 10,7 | 2,6 | 7,7 |
Вариант № 29. При изучении зависимости между производительностью Y (тн / чел.) труда и дебитом X (тн / сут.) скважин получены следующие результаты:
| X | ||||||||||
| Y | 30,8 | 31,5 | 33,5 | 32,5 | 31,2 |
Вариант № 30. При исследовании зависимости времени t (с), затрачиваемого на закрепление детали, от ее веса P (кг) получены следующие результаты:
| P | ||||||||||
| t | 30,8 | 31,5 | 33,5 | 32,5 | 31,2 |
Поиск по сайту: