АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Проверка наличия зависимости между номинальными признаками. (Таблицы сопряженности)

Читайте также:
  1. I. Личные отношения между супругами
  2. II. Имущественные отношения между супругами
  3. II. Личные отношения между родителями и детьми, законными и другими
  4. III. Другие виды вещей, или имуществ, в зависимости от свойств вещей в гражданском обороте
  5. IV Международного фестиваля-конкурса
  6. IV Международный конкурс эссе на русском и английском языках
  7. Review: Формальные показатели наличия в предложениях степеней сравнения
  8. VII. Международные отношения
  9. VII. Министерствам и ведомствам по молодежной политике стран-участниц Международной конференции
  10. X. Параллельная сессия 5 - Международная конференция «Энергетический потенциал отходов»
  11. Акт балансовой принадлежности и эксплуатационной ответственности между общим имуществом многоквартирного дома и помещением Собственника
  12. Актуализация опорных знаний. Проверка д/з.

 

1.Смоделируйте две выборки 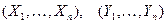из нормального распределения с произвольными математическими ожиданиями 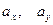и произвольными дисперсиями 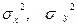. (Положите, например, n=50).

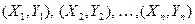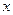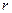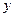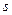Построим двумерную выборку из двух смоделированных выборок: . Разобьем ось на непересекающихся промежутков, а ось на непересекающихся промежутков.

В результате можем считать, что имеется два номинальных признака - признак 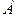имеет 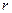уровней 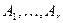, признак 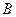имеет 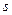уровней 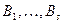, можно считать, что имеется выборка случайно отобранных 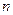объектов из генеральной совокупности, по которой нужно найти частоты совместной встречаемости событий .

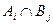Частоты следует собрать в таблицу, называемую таблицей сопряженности. Выборочные частоты совместной встречаемости различных градаций двух признаков запишем в таблицу сопряженности признаков 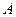и .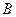

 

 
 

 

, , .

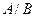
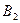
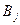
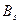
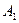
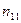
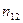
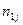
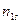
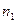
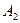
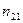
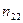
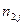
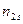
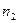
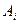
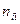
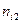
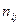
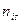
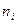
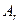
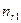
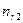
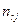
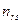
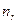
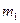
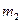
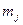
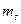
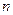
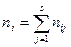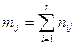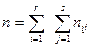Положим , , .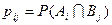

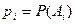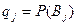Формулировка гипотезы о независимости признаков 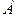и :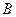

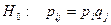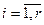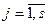, , . При этом , .

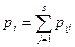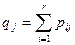Метод проверки гипотезы 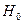основан на статистиках:

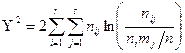
Если признак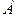и и 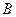(имеющие 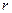и 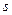уровней соответственно) независимы, то статистик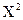и и 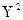имеют (приближенно, при большом числе 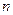) распределение 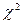с с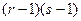тепенями свободы.

 

Величины 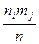называют ожидаемыми частотами (ожидаемыми при выполнении гипотезы) появления события .

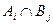При этом величина 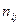представляет собой наблюдаемую в опыте частоту события 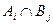. Считается достаточным, чтобы по всем ячейкам ожидаемые частоты были бы не меньше 3.

Таким образом, при больших :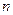

· для независимых признаков статистика 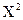асимптотически распределена по закону 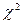с с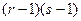тепенями свободы.

· для зависимых признаков 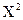неограниченно возрастает при увеличении .

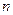Для проверки гипотезы 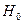на уровне значимости 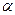необходимо вычислить одну из статистик 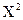(или 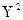) и сравнить ее значение с соответствующим критическими значениям 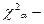верхняя квантиль уровня 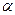из распределения 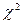с с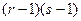тепенями свободы, квантиль можно найти из таблиц математической статистики или с помощью функции ХИ2ОБР при этом:

· принимаем 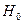, если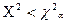

· отвергаем 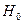, если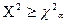

2. По смоделированным выборкам постройте таблицу сопряженности, выбрав .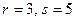

Проверьте гипотезу о независимости номинальных признаков, используя каждую из двух статистик. Напишите отчет.

3. Попробуйте найти содержательные данные, например в Интернете, для проверки наличия взаимосвязи признаков с помощью таблиц сопряженности.

 

Оформите отчет по всем выполненным заданиям. (Отчет оформляется в MS Word 2003 или в подобном редакторе)

 

 


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)