 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основные сведения из теории
СТАТИКА
Определение реакций опор при действии плоской произвольной системы сил
Основные сведения из теории
Плоской произвольной системой сил называется система сил, линии действия которых лежат в одной плоскости (рис. 10, а).


Рис. 10
Любую такую систему сил можно упростить, приведя ее к произвольному центру (рис. 10, б).
При этом в центре приведения будут приложены два вектора: главный вектор  , равный геометрической сумме всех сил системы и главный момент
, равный геометрической сумме всех сил системы и главный момент  , равный геометрической сумме моментов всех сил системы относительно центра приведения. При любом значении главного момента системы, кроме нулевого, его вектор перпендикулярен плоскости, содержащей силы системы. Поэтому в случае плоской произвольной системы сил принято говорить об алгебраическом моменте и на рисунке показывать только направление поворота (рис. 10, в).
, равный геометрической сумме моментов всех сил системы относительно центра приведения. При любом значении главного момента системы, кроме нулевого, его вектор перпендикулярен плоскости, содержащей силы системы. Поэтому в случае плоской произвольной системы сил принято говорить об алгебраическом моменте и на рисунке показывать только направление поворота (рис. 10, в).


Рис. 10, в Рис. 11
Алгебраическим моментом силы относительно точки (центра) называется произведение модуля силы на плечо.
Если сила  стремится повернуть тело вокруг точки О против хода часовой стрелки, то момент положителен, если же по ходу часовой стрелки, то отрицателен
стремится повернуть тело вокруг точки О против хода часовой стрелки, то момент положителен, если же по ходу часовой стрелки, то отрицателен  ,
,  (рис. 11). Момент силы относительно точки (центра) равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю,
(рис. 11). Момент силы относительно точки (центра) равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю,  (рис. 11).
(рис. 11).
Система двух параллельных сил, равных по модулю и направленных в разные стороны, называется парой сил (рис. 12 и 13).

Рис. 12 Рис. 13
Кратчайшее расстояние между линиями действия этих сил называется плечом пары. Так как две силы, равные по модулю и направленные в разные стороны, не лежат на одной линии действия, то тело, к которому приложена пара сил, не находится в равновесии. Мерой действия пары сил является величина, называемая ее моментом. Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары на плечо. Если пара сил стремится повернуть тело против хода часовой стрелки, то момент пары положителен, (рис. 12); если по ходу часовой стрелки, то отрицателен (рис. 13). Пара сил может быть уравновешена только парой сил.
При рассмотрении плоской произвольной системы сил пару сил показывают условной парой или направлением поворота (рис. 14).
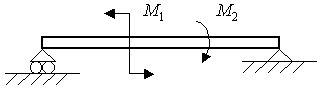
Рис. 14
Для плоской произвольной системы сил необходимыми и достаточными условиями равновесия являются равенство нулю главного вектора и главного момента системы относительно центра приведения:
 .
.
Этим двум условиям равновесия соответствуют три уравнения равновесия, два из которых – уравнения проекций главного вектора на систему отсчета и третье уравнение моментов относительно центра приведения:
 ,
,
 , - основная или первая форма уравнений равновесия.
, - основная или первая форма уравнений равновесия.

Существуют еще две формы уравнений равновесия: вторая, содержащая одно уравнение проекции главного вектора и два уравнения моментов сил системы относительно двух центров приведения:
 ,
,
 , - вторая форма уравнений равновесия.
, - вторая форма уравнений равновесия.

Эта система уравнений равновесия имеет ограничения: ось, на которую проецируются все силы системы не может быть перпендикулярна отрезку, соединяющему центры приведения (рис. 15, а).
а) б) С
a
А В
А В
х
Рис. 15
Третья форма уравнений равновесия плоской произвольной системы сил содержат три уравнения моментов сил системы относительно трех центров приведения:
 ,
,
 , - третья форма уравнений равновесия.
, - третья форма уравнений равновесия.

Она тоже имеет ограничения: центры приведения не должны лежать на одной прямой (рис. 15, б).
Плоской параллельной системе сил соответствуют две формы уравнений равновесия:
1)  , 2)
, 2)  ,
,
 .
.  .
.
Распределенная нагрузка характеризуется интенсивностью q, то есть нагрузкой, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в нъютонах, деленных на метры.
Равнодействующая численно равна площади графика, занимаемого нагрузкой.
Приведем некоторые примеры распределенных сил, лежащих в одной плоскости (рис. 16).
а) б)

Рис. 16
1. Силы, равномерно распределенные вдоль нагруженного отрезка прямой (рис.16, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей 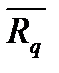 , которая численно равна площади прямоугольника, высота которого q, а основание l.
, которая численно равна площади прямоугольника, высота которого q, а основание l.
 .
.
Приложена 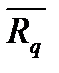 в точке, проходящей через центр тяжести прямоугольника, т.е. делит основание АВ пополам.
в точке, проходящей через центр тяжести прямоугольника, т.е. делит основание АВ пополам.
2. Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 16, б). Равнодействующая Rq численно равна площади треугольника АВС:
 .
.
и приложена на расстоянии  от стороны ВС.
от стороны ВС.
При решении задач иногда полезно использовать теорему Вариньона, которая формулируется следующим образом: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О равен сумме моментов сил системы относительно того же центра.
Задача 1. Определить реакции RA и RB опор балки, размеры и нагрузки которой показаны на рис.18, а.


Рис. 18
Решение. 1. Составление расчетной схемы. Объект равновесия – балка АС. Активные силы: F = 3 кH, пара сил с M = 4 кH∙м распределенная нагрузка с интенсивностью q = 1 кН/м, которуюзаменяем одной сосредоточенной силой Rq = q∙ 1 = 1 ∙ 3 = 3 кH; приложенной к точке D на расстоянии 1,5 м от края консоли. Применяя принцип освобождаемости от связей изобразим в точках А и В реакции. На балку действует плоская произвольная система сил, в которой три неизвестных реакции  и
и  .
.
Ось х направим вдоль горизонтальной оси балки вправо, а ось у -вертикально вверх.
2. Условия равновесия:
 .
.
3. Составление уравнений равновесия:
 ,(1)
,(1)
 , (2)
, (2)
 . (3)
. (3)
4. Определение искомых величин, проверка правильности решения и анализ полученных результатов. Решая систему уравнений (1 – 3), определяем неизвестные реакции
из (1):
 кН,
кН,
из (3):  ,
,
из (2):  кН.
кН.
Величина реакции RAх имеет отрицательный знак, значит направлена не так, как показано на рис. 18, а в противоположную сторону.
Для проверки правильности решения составим уравнение суммы моментов относительно точки Е.
 .
.
Подставив в это уравнение значения входящих в него величин, получим:
- 0,58 ∙ 1 – 4 + 5,02 ∙ 3 – 3 ∙ 3,5 = 0.
Уравнение удовлетворяется тождественно, что подтверждает правильность решения задачи.
Задача 2. На балку с защемленным концом (рис. 19, а) действует распределенная по линейному закону нагрузка интенсивностью q = 0,2 кН/м. Сила F = 10 кH действует под углом α = 45о к оси балки, кроме того, приложена пара сил с моментом М = 4 кH ∙м. Определить реакцию заделки.
а) б)


Рис.19
Решение.
1. Составление расчетной схемы (рис. 19, б). Объектом равновесия является балка АВ. К ней приложены активные силы  , пара сил с моментом
, пара сил с моментом  ираспределенная по линейному закону нагрузка. Равнодействующая
ираспределенная по линейному закону нагрузка. Равнодействующая  приложена в точке О,
приложена в точке О, 
Связью, наложенной на балку АВ,является жесткая заделка А. Применяя принцип освобождаемости от связей к балке АВ,заменим действие этой заделки на балку силами реакций  и
и  реактивным моментом
реактивным моментом 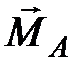 . Рассмотрим теперь равновесие балки АВ как свободного твердого тела, на которое действуют, кроме активных сил, еще и реакции связи.
. Рассмотрим теперь равновесие балки АВ как свободного твердого тела, на которое действуют, кроме активных сил, еще и реакции связи.
2. Усл овия равновесия:
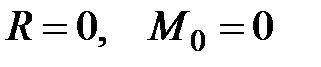 .
.
3. Составление уравнений равновесия. Для плоской произвольной
системы сил условиям равновесия соответствуют три уравнения:
 ; (а)
; (а)
 ; (б)
; (б)
 . (в)
. (в)
Для балки с жёсткой заделкой в качестве моментальной точки лучше брать заделку, что позволит исключить лишние неизвестные.
4. Определение искомых величин, проверка правильности решения и анализ полученных результатов.
Из уравнения (а) находим:
 .
.
Из уравнения (б) получаем:
 .
. 
Наконец, из уравнения (в) находим:

Проверка. Составим уравнение моментов относительно точки В, подставим найденные реакции:
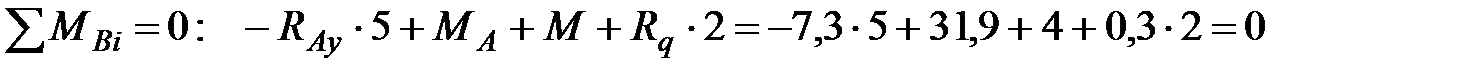 .
.
Положительные значения реакций связей подтверждают правильность выбранных направлений этих сил.
КИНЕМАТИКА
Задача 1. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени  , найти положение точки на траектории, ее скорость, касательное, нормальное и полное ускорения, а также радиус кривизны траектории:
, найти положение точки на траектории, ее скорость, касательное, нормальное и полное ускорения, а также радиус кривизны траектории:
 , (1)
, (1)
где Х и Y в сантиметрах, t – в секундах.
Решение. 1. Определение уравнения траектории. Параметрическим представлением траектории является сам закон движения. Уравнение траектории в координатной форме получаем, исключая из закона движения время:
 .
.
Получили  , то есть траекторией точки является парабола. Для построения траектории рассчитаем по уравнениям координаты точек параболы, отвечающие нескольким моментам времени. Результаты расчетов приведены в таблице 3.
, то есть траекторией точки является парабола. Для построения траектории рассчитаем по уравнениям координаты точек параболы, отвечающие нескольким моментам времени. Результаты расчетов приведены в таблице 3.
Таблица 3
| t, с | 0,5 | ||
| X, cм | |||
| Y, см | - 1 |
Траектория построена на рис. 12, на ней стрелкой показано направление движения точки из начального положения при  с координатами
с координатами  .
.
2. Определение скорости. Дифференцируя (1) по времени, находим проекции скорости точки на оси координат Х, Y:
 . (2)
. (2)
При 

 .
.

Рис. 12
По найденным проекциям определяем модуль скорости:
 .
.
3. Определение ускорения. Дифференцируя (2), находим проекции вектора ускорения:
 .
.
При 
 .
.
По найденным проекциям определяем модуль ускорения:

4. Определение касательного ускорения при  :
:
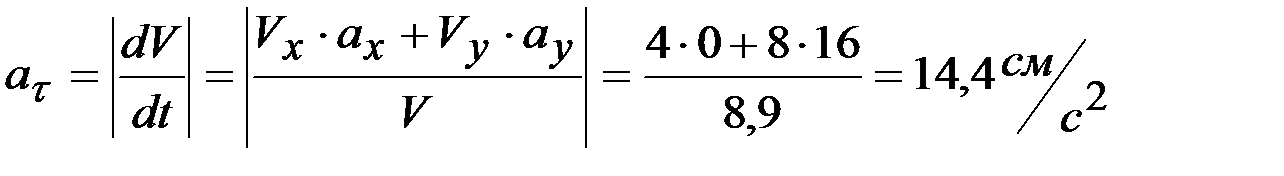 .
.
5. Определение нормального ускорения при  :
:
 .
.
6. Определение радиуса кривизны при  :
:
 .
.
Результаты вычислений для заданного момента времени  приведены в таблице 4.
приведены в таблице 4.
Таблица 4
| Координаты, см | С к о р о с т ь,

| Ус к о р е н и е,

| Радиус кривизны, см | |||||||
| Х | Y | Vx | Vy | V | ax | ay | a | at | an | r |
| 8,9 | 14,4 | 6,9 | 11,6 |
На рис. 12 показано положение точки М в заданный момент времени.
Векторы скорости и ускорения в этой точки построены в масштабе по их проекциям на оси координат:  , там же показаны касательное и нормальное ускорения. Совпадение величин at и an, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
, там же показаны касательное и нормальное ускорения. Совпадение величин at и an, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
Радиус кривизны проведен в сторону вогнутости траектории перпендикулярно к вектору скорости – по направлению an.
Задача 2. По заданному уравнению прямолинейного поступательного движения груза 1  , см определить скорость, а также вращательное, центростремительное и полное ускорение точки М механизма в момент времени, когда путь, пройденный грузом равен S. R 2 = 50 см; r 2 = 30 см; R 3 = 60 см; r 3 = 40 см; S = 50 см (рис. 17).
, см определить скорость, а также вращательное, центростремительное и полное ускорение точки М механизма в момент времени, когда путь, пройденный грузом равен S. R 2 = 50 см; r 2 = 30 см; R 3 = 60 см; r 3 = 40 см; S = 50 см (рис. 17).

Рис. 17
Решение. 1. Кинематический анализ. Механизм состоит из трех тел: груз 1 совершает поступательное движение, а колеса 2 и 3 вращаются вокруг неподвижных осей, перпендикулярных плоскости чертежа. Связи между телами идеальны. Определим момент времени t, когда путь S, пройденный грузом равен 50 см:
 ,
,
откуда
 .
.
Скорость груза определим дифференцированием по времени уравнения движения:
 .
.
2. Определение угловых параметров колес 2 и 3.
Угловая скорость колеса 2
 .
.
Угловые скорости колес 2 и 3, связанных гибкой передачей, обратно пропорциональны радиусам этих колес, то есть
 ,
,
откуда
 .
.
Угловое ускорение колеса 3
 .
.
3. Определение линейных параметров.
Скорость точки М колеса 3

и направлена перпендикулярно к радиусу в сторону вращения колеса 3.
Вращательное ускорение точки М
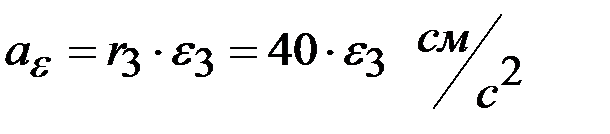
и имеет одинаковое со скоростью направление, так как вращение колес ускоренное (угловая скорость и угловое ускорение имеет одинаковые знаки).
Центростремительное ускорение точки М

и направлено по радиусу к центру колеса.
Полное ускорение
 .
.
Значение всех определяемых величин для времени  представлены в таблице, а направление скоростей и ускорений точки М показаны на рис. 18.
представлены в таблице, а направление скоростей и ускорений точки М показаны на рис. 18.
Таблица 5

| 
| 
| У с к о р е н и е, 
| ||
| аε | аω | а | |||
| 2,75 | 2,75 | 756,3 | 764,26 |
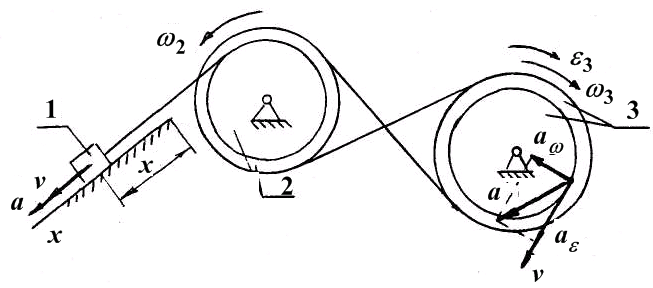
Рис. 18
ДИНАМИКА
Задача 1. В железнодорожных скальных выемках для защиты кюветов от попадания в них с откосов каменных осыпей устраивается «полка» DC. Учитывая возможность движения камня из наивысшей точки А откоса и полагая при этом его начальную скорость  , определить наименьшую ширину полки b и скорость
, определить наименьшую ширину полки b и скорость  , с которой камень падает на нее. По участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l, камень движется τ с. Коэффициент трения скольжения f камня на участке АВ считать постоянным, а сопротивлением воздуха пренебречь. Дано:
, с которой камень падает на нее. По участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l, камень движется τ с. Коэффициент трения скольжения f камня на участке АВ считать постоянным, а сопротивлением воздуха пренебречь. Дано:  . Определить b и
. Определить b и  (рис. 3.7).
(рис. 3.7).

Рис. 3.7
Решение. Задачу разделим на два этапа. Первый – движение камня на участке АВ, второй – движение камня от точки В до С.
Первый этап. 1. Составление расчетной схемы. Ось  проводим по направлению движения камня, ось
проводим по направлению движения камня, ось  - перпендикулярно к оси
- перпендикулярно к оси  . Камень принимаем за материальную точку и показываем ее в текущем положении, изображаем действующие на камень (точку) силы: вес
. Камень принимаем за материальную точку и показываем ее в текущем положении, изображаем действующие на камень (точку) силы: вес  , нормальную реакцию
, нормальную реакцию  и силу трения скольжения
и силу трения скольжения  (рис. 3.8).
(рис. 3.8).
2. Выявление начальных условий. При  .
.

Рис. 3.8
3. Составление дифференциальных уравнений движения точки. Так как точка (камень) движется прямолинейно, то при направлении оси х вдоль траектории получим одно дифференциальное уравнение движения
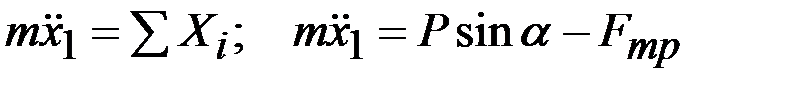 ;
;
сила трения
 ,
,
тогда
 ;
;
 ;
;
 .
.
4. Интегрирование дифференциальных уравнений движения. Интегрируя дифференциальное уравнение дважды, получаем:
 ;
;
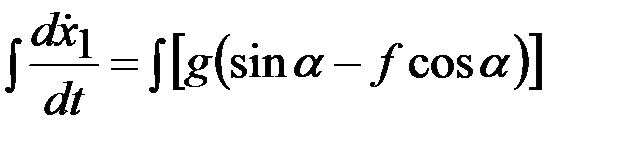 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
5. Определение постоянных интегрирования. Подставим начальные условия, т.е.  в уравнения:
в уравнения:
 ;
;
 ;
;

 .
.
6. Нахождение неизвестных величин и исследование полученных результатов. После подстановки постоянных интегрирования С 1 и С 2 получаем уравнение скорости и уравнение движения:
 ;
;
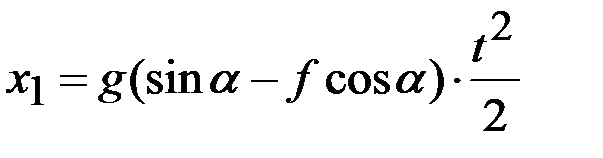 .
.
Для момента времени τ, когда камень покидает участок АВ,
 ,
,
т.е.
 ;
;
 .
.
Умножим первое уравнение на τ/ 2, после этого разделим его на второе. В результате получим:
 ;
; 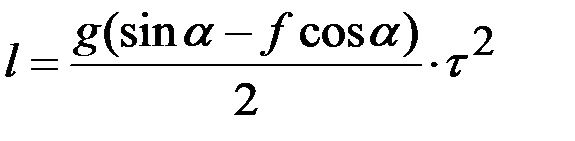 ;
;
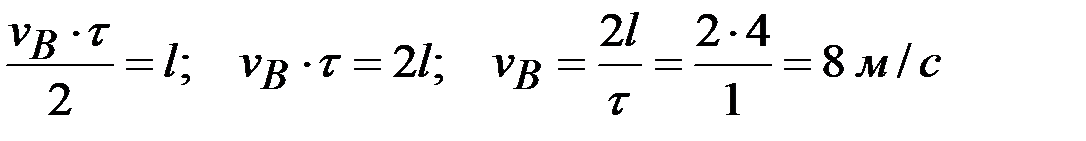 .
.
Второй этап: движение камня от точки В до точки С.
1. Составление расчетной схемы. Координатные оси покажем так, как это удобно для решения задачи, в нашем случае ось х параллельна горизонтали и проходит через точку В, ось у направляем вниз через точку В. Камень принимаем за материальную точку, показываем ее в текущем положении, изображаем действующую на камень силу тяжести  (рис. 3.8).
(рис. 3.8).
2. Выявление начальных условий движения. При  :
: 
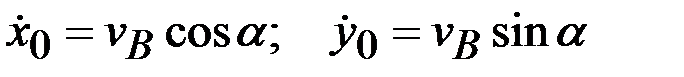 .
.
3. Составление дифференциальных уравнений движения. Так как движение точки происходит в плоскости ху, то число уравнений движения равно двум:
 .
.
4. Интегрирование дифференциальных уравнений движения. Интегрируем дифференциальные уравнения дважды:
 (a)
(a)
 ; (б)
; (б)
 (в)
(в)
 . (г)
. (г)
5. Определение постоянных интегрирования. Подставляем начальные условия:  в уравнения (а – г):
в уравнения (а – г):

 ,
,
откуда
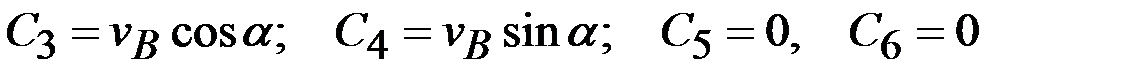 .
.
6. Нахождение искомых величин и исследование полученных результатов. После подстановки постоянных интегрирования в уравнения (а –г) получаем следующие уравнения проекций скорости камня:

и уравнения его движения
 .
.
Уравнение траектории камня найдем, исключив параметр t из уравнений движения:
 ;
;
 – уравнение параболы.
– уравнение параболы.
В момент падения 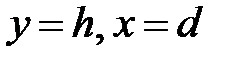 . Определим d из уравнения траектории:
. Определим d из уравнения траектории:
 ;
;  ;
;
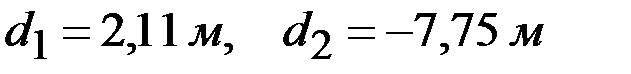 .
.
Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то d =2,11 м.
Минимальная ширина полки
 .
.
Используя уравнение движения камня  , найдем время Т движения камня от точки В до точки С
, найдем время Т движения камня от точки В до точки С
 .
.
Скорость камня при падении найдем через проекции скорости на оси координат:

по формуле
 .
.
Для момента падения t=T= 0,53 c
 .
.
Скорость камня при падении равна 12,8 м/с.
Задача 2. Механизм, состоящий из груза А массой 50 кг, блока В массой 80 кг (больший радиус R = 30 см, меньший r = 10 см) и цилиндра С массой 120 кг радиусом RC = r /2, установлен на призме D массой 210 кг, находящейся на горизонтальной плоскости. Трение между призмой и плоскостью отсутствует. Груз А получает перемещение S = 1,2 м относительно призмы вдоль ее поверхности влево; α = 75° (рис. 124). Куда и на какое расстояние переместится призма?
Решение.
Задаем систему координат. Проекции на горизонтальную ось всех внешних сил (сил тяжести GA, GB, GC, GD, реакции опоры N), действующих на систему, равны нулю (рис. 125), а трения между призмой D и опорой по условию нет. Применим к системе следствие из теоремы о движении центра масс



Рис. 124 Рис. 125
1. Абсолютное смещение тел А, В и С представляем как сумму относительного смещения, зависящего от величины S относительного смещения груза А, и неизвестного переносного смещения AD, равного абсолютному смещению призмы, относительно которой задавалось смещение S. Обозначаем абсолютные смещения координат центров масс тел системы Δ А, Δ B, Δ C, Δ D. Направление оси х определяет знаки смещений: налево с минусом, направо с плюсом. Предполагаем, что призма сместится направо. Перемещение центра цилиндра С относительно призмы и перемещение груза А связаны так же, как связаны их скорости.
Цилиндр С совершает плоское движение. Абсолютное смещение его центра в проекции на ось х равно Δ D — SC cos α, где SC — смещение центра цилиндра вдоль наклонной поверхности призмы. Выразим SC через S. Для этого свяжем скорости груза А и центра масс цилиндра С. Мгновенный центр скоростей цилиндра находится в точке касания призмы, поэтому скорость его центра масс относительно призмы вдвое меньше скорости нити, накручиваемой на обод. Скорость груза А выражаем через угловую скорость блока (рис. 132, с. 249):
 . (5)
. (5)
Исключая отсюда  , имеем связь скоростей:
, имеем связь скоростей:  . Интегрируя это соотношение при нулевых начальных значениях, получаем искомую зависимость: SC =0,5 Sr / R. Находим выражение абсолютных смещений всех тел через Δ D, и S:
. Интегрируя это соотношение при нулевых начальных значениях, получаем искомую зависимость: SC =0,5 Sr / R. Находим выражение абсолютных смещений всех тел через Δ D, и S:
 . (6)
. (6)
2. Подставляя абсолютные смещения в (4), получаем уравнение
 ,
,
или
 .
.
Решаем это уравнение относительно Δ D:
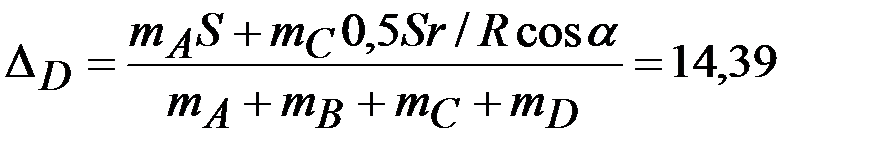 .
.
Призма D переместится вправо на 14.39 см.
Поиск по сайту: