АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Реализация множеств через бинарные деревья поиска. Эффективность основных операций

Читайте также:
  1. C. Множественные пятна на коже, цвет которых варьирует от белого до бурого
  2. C. Через 10 – 30 мин и длится 1 – 2 часа
  3. C.2. Множественная регрессия и корреляция
  4. Exercises for Lesson 2. Possessions / Личные вещи. Лексика. Множественное число. Притяжательные прилагательные. Притяжательные местоимения.
  5. Exercises for Lesson 2. Possessions / Личные вещи. Лексика. Множественное число. Притяжательные прилагательные. Притяжательные местоимения.
  6. А расчётных операций.
  7. Адекватность понимания связи свойств нервной системы с эффективностью деятельности
  8. Акцизы: налогоплательщики и объекты налогообложения. Особенности определения налоговой базы при перемещении подакцизных товаров через таможенную границу РФ.
  9. Алгоритм проверки адекватности множественной регрессионной модели (сущность этапов проверки, расчетные формулы, формулировка вывода).
  10. Алгоритм проверки значимости регрессоров во множественной регрессионной модели: выдвигаемая статистическая гипотеза, процедура ее проверки, формулы для расчета статистики.
  11. Амортизация основных фондов
  12. Анализ динамического ряда. Вычисление основных показателей динамического ряда

Понятие множества как структуры данных и его свойства

Множеством называется совокупность однотипных элементов, рассматриваемых как единое целое.

Свойства:

1) Уникальность элементов

2) Возможность добавления элементов

3) Удаление элементов

4) Объединение множеств

5) Проверка на принадлежность

Байт: (состоит из 8 бит) (его части это элементы множества)

Если внутри все элементы будут равны нулю, то множество пустое. Если единице, тогда это Универсум.

-универсум (все с нулями – пустое множество)

Главный минус – выделение большого количества памяти, даже если она не расходуется.

Способ проверки на наличие нужного элемента в множестве – наложение маски.

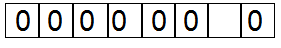Накладываем маску (если в пустом месте появится 1, то элемент присутствует)

Реализация множеств через битовые карты. Эффективность основных операций.

Битовая карта - набор последовательно записанных двоичных разрядов, то есть последовательность (массив) битов.

Метод битовых карт. Этот метод подходит лишь для элементов, чьи значения могут быть представлены целыми числами в ограниченном диапазоне. Если мы знаем максимально возможное значение элемента в списке (Nmax), то мы можем создать битовую карту, содержащую Nmax -битов. Затем проходимся по всем элементам списка, устанавливая соответствующий бит в карте для каждого элемента. После этого подсчитываем количество установленных битов.
Метод битовых карт начинает тормозить, когда битовая карта перестает помещаться в оперативной памяти. А для малого кол-ва элементов этот метод эффективен.

 

 

Реализация множеств через бинарные деревья поиска. Эффективность основных операций.

Бинарные деревья поиска обычно применяются для реализации множеств и ассоциативных массивов.. И применяются для быстрого поиска информации. Двоичные деревья, как и связные списки, являются рекурсивными структурами.

Реализация множества с помощью бинарного поиска во всех отношениях лучше наивной реализации. Вместе с тем, она все же имеет недостатки: 1) при добавлении и удалении элементов в середине массива приходится переписывать элементы в конце массива на новое место, чтобы освободить место для добавляемого элемента либо закрыть образовавшуюся лакуну при удалении элемента; 2) поиск выполняется гарантированно быстро, но все-таки не мгновенно. Первый недостаток можно устранить, применяя ссылочную реализацию. Чтобы поиск выполнялся быстро, дерево должно быть сбалансированным, т.е. все его ветви должны иметь почти одинаковую длину.

 


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)