 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Числовые множества
Примеры числовых множеств: 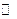 - множество натуральных чисел,
- множество натуральных чисел,  - множество целых чисел,
- множество целых чисел, 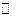 - множество рациональных чисел,
- множество рациональных чисел,  - множество вещественных чисел. Очевидно, что
- множество вещественных чисел. Очевидно, что 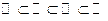 .
.
Множества, состоящие из конечного числа элементов, называются конечными множествами. Два конечных множества мы можем сравнивать по числу элементов и судить, одинаково ли это число или же в одном из множеств элементов больше чем в другом. Таким образом, мы считаем число элементов в каждом из них и сравниваем. Но можно поступить иначе: попытаться установить биекцию (bij), т.е. взаимно однозначное соответствие между элементами этих множеств (соответствие, при котором каждому элементу одного множества отвечает один и только один элемент другого, и наоборот). Ясно, что взаимно однозначное соответствие можно установить между двумя конечными множествами тогда и только тогда, когда число элементов в них одинаково. Например, чтобы проверить, одинаково ли число студентов в группе и стульев в аудитории, можно, не пересчитывая тех и других, посадить каждого студента на определённый стул. Если всем хватит мест и не останется лишних стульев, т.е. будет установлена биекция между множеством стульев и множеством студентов, то число элементов у этих множеств одинаково.
Подсчёт числа элементов в множестве годится лишь для сравнения конечных множеств, а установление биекции между множествами годится и для бесконечных множеств.
Простейшим среди бесконечных множеств является множество натуральных чисел 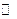 .
.
Определение. Два множества 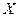 и
и 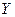 называются эквивалентными или равномощными (
называются эквивалентными или равномощными ( ), если существует биективное отображение
), если существует биективное отображение 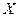 на
на 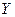 :
:
 .
.
Из этого определения вытекают следующие отношения эквивалентности:
1) рефлексивность: 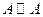 ,
,
2) симметричность: если 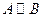 , то
, то 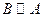 ,
,
3) транзитивность: если 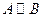 и
и  , то
, то 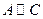 ,
,
где  - произвольные множества.
- произвольные множества.
Например, множество натуральных чисел эквивалентно множеству, состоящему из чётных натуральных чисел: 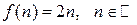 .
.
Определение. Множество 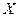 называется счётным, если оно эквивалентно (равномощно) множеству натуральных чисел:
называется счётным, если оно эквивалентно (равномощно) множеству натуральных чисел:  - счётно, если
- счётно, если  .
.
Примеры. 1. Покажем, что множество целых чисел счётно, т.е. что  .
.
Зададим биективное отображение  по правилу:
по правилу:
 , где
, где 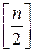 - целая часть числа
- целая часть числа 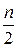 .
.
Напомним, что если число 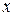 представить в виде
представить в виде  , где
, где  , а
, а 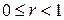 , то
, то  - целая часть числа
- целая часть числа 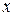 ,
, 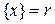 - дробная часть числа
- дробная часть числа 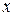 .
.
Замечание. Если множество 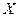 - счётно, то каждому элементу
- счётно, то каждому элементу 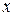 этого множества соответствует некоторое натуральное число
этого множества соответствует некоторое натуральное число 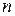 . Обозначим этот элемент
. Обозначим этот элемент  , а
, а 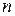 будем считать его номером. Таким образом, множество счётно, если все его элементы можно перенумеровать натуральными числами.
будем считать его номером. Таким образом, множество счётно, если все его элементы можно перенумеровать натуральными числами.
2. Покажем, что множество рациональных чисел счётно, т.е. что  .
.
Каждое рациональное число 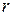 представим в виде несократимой дроби
представим в виде несократимой дроби 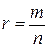 , где
, где 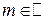 ,
,  . Рассмотрим таблицу:
. Рассмотрим таблицу:
0 1 -1 2 -2 3 -3 4 ……
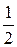
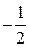


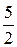

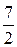
 ……
……
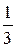


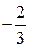
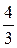
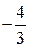
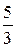
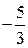 ……,
……,
……………………………………………………………
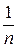
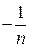 ………………………………………………
………………………………………………
……………………………………………………………
где 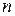 -ая строка составлена из несократимых рациональных чисел со знаменателем
-ая строка составлена из несократимых рациональных чисел со знаменателем 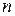 , расположенных по возрастанию их абсолютных величин, причём за каждым положительным числом следует ему противоположное. Таким образом, каждое рациональное число находится на каком-то месте этой таблицы. Занумеруем элементы таблицы следующим способом:
, расположенных по возрастанию их абсолютных величин, причём за каждым положительным числом следует ему противоположное. Таким образом, каждое рациональное число находится на каком-то месте этой таблицы. Занумеруем элементы таблицы следующим способом:
1 2 4 7 ……
3 5 8 ….………..
6 9 …………………
10……………………..……
…………………………….
Все рациональные числа занумерованы. Следовательно, множество  - счётно.
- счётно.
Лемма 1. Любое бесконечное множество содержит счётное подмножество.
Доказательство. Пусть  - бесконечное множество. Следовательно,
- бесконечное множество. Следовательно, 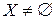 и найдется элемент, принадлежащий данному множеству, который обозначим
и найдется элемент, принадлежащий данному множеству, который обозначим 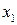 . Так как множество
. Так как множество  бесконечно, то множество
бесконечно, то множество  \
\ 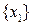 не пусто и в нём найдётся элемент, который обозначим
не пусто и в нём найдётся элемент, который обозначим  . Так как множество
. Так как множество  бесконечно, то множество
бесконечно, то множество  \
\  и в нём найдётся элемент, который обозначим
и в нём найдётся элемент, который обозначим  . Поступая аналогичным образом, получим на
. Поступая аналогичным образом, получим на 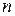 -ом шаге, что существует элемент
-ом шаге, что существует элемент  :
: 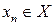 \
\  . И так далее. Таким образом, мы построили счётное множество
. И так далее. Таким образом, мы построили счётное множество 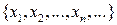 которое является подмножеством исходного бесконечного множества
которое является подмножеством исходного бесконечного множества  . Лемма доказана.
. Лемма доказана.
Лемма 2. Любое бесконечное подмножество счётного множества счётно.
Доказательство. Пусть  - счётное множество, т.е. его можно представить в виде
- счётное множество, т.е. его можно представить в виде 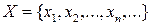 . Пусть
. Пусть 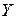 - любое бесконечное подмножество множества
- любое бесконечное подмножество множества  (
(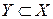 ). Обозначим через
). Обозначим через 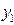 тот элемент множества
тот элемент множества 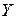 , который имеет наименьший номер в множестве
, который имеет наименьший номер в множестве  , через
, через  тот элемент множества
тот элемент множества 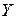 , который имеет ближайший номер к
, который имеет ближайший номер к 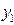 в множестве
в множестве  . Так как
. Так как 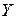 - бесконечное множество, то процесс нумерации бесконечен, а следовательно,
- бесконечное множество, то процесс нумерации бесконечен, а следовательно, 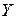 - счётное множество. Лемма доказана.
- счётное множество. Лемма доказана.
Лемма 3. Объединение счётного семейства счётных множеств счётно. Доказательство. Пусть 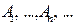 - счётные множества. Обозначим их через
- счётные множества. Обозначим их через 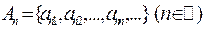 . Тогда объединение этих множеств
. Тогда объединение этих множеств  состоит из элементов
состоит из элементов 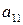
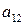
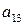 …
…
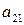
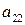
 …
…
………………..
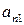
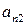
 …
…
………………..
Таким образом, все элементы множества  занумерованы, а, следовательно, оно является счётным. Лемма доказана.
занумерованы, а, следовательно, оно является счётным. Лемма доказана.
Определение. Конечное или счётное множество называется не более чем счётным.
Определение. Множество  (
(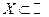 ) называется ограниченным сверху, если
) называется ограниченным сверху, если
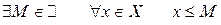 .
.
Число 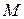 называется верхней гранью множества
называется верхней гранью множества  .
.
Множество  (
(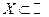 ) называется ограниченным снизу, если
) называется ограниченным снизу, если
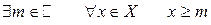 .
.
Число 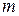 называется нижней гранью множества
называется нижней гранью множества  .
.
Множество  (
(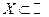 ) называется ограниченным, если оно ограничено и сверху, и снизу:
) называется ограниченным, если оно ограничено и сверху, и снизу: 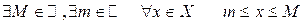
или
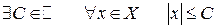 .
.
Примеры. 1. Множество  ограничено снизу любым неположительным числом.
ограничено снизу любым неположительным числом.
2. Множество 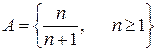 ограничено сверху любым числом, больше либо равным 1, и ограничено снизу любым числом, меньше либо равным
ограничено сверху любым числом, больше либо равным 1, и ограничено снизу любым числом, меньше либо равным 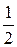 .
.
3. Множество  ограничено сверху любым числом, больше либо равным 1, и ограничено снизу любым неположительным числом.
ограничено сверху любым числом, больше либо равным 1, и ограничено снизу любым неположительным числом.
Определение. Пусть множество  (
(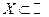 ) ограничено сверху. Наименьшее среди всех чисел, ограничивающих сверху множество
) ограничено сверху. Наименьшее среди всех чисел, ограничивающих сверху множество  , называется его точной верхней гранью и обозначается
, называется его точной верхней гранью и обозначается 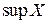 (супремум множества
(супремум множества  ).
).
Пример. Для множеств 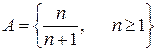 и
и 
 .
.
Супремум множества  совпадает с его максимальным элементом (
совпадает с его максимальным элементом ( ).
).
Из определения следует, что

или 
Определение. Пусть множество  (
(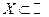 ) ограничено снизу. Наибольшее среди всех чисел, ограничивающих снизу множество
) ограничено снизу. Наибольшее среди всех чисел, ограничивающих снизу множество  , называется его точной нижней гранью и обозначается
, называется его точной нижней гранью и обозначается  (инфимум множества
(инфимум множества  ).
).
Пример. 1.  .
.
2. Для множеств 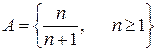 и
и 
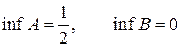 .
.
Инфимумы множеств  и
и  совпадают с их минимальными элементами (
совпадают с их минимальными элементами (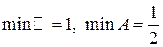 ).
).
Из определения следует, что
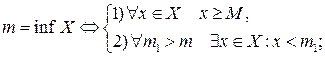
или 
Заметим, что 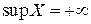 , если множество
, если множество  не ограничено сверху и
не ограничено сверху и 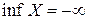 , если множество
, если множество  не ограничено снизу.
не ограничено снизу.
Так, например, 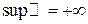 ,
,  .
.
Теорема (свойство непрерывности множества действительных чисел). Пусть 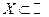 ,
, 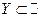 ,
, 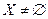 ,
,  и
и  .
.
Тогда 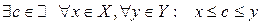 .
.
Теорема (принцип Кантора вложенных сегментов). Пусть  - система отрезков, удовлетворяющих условиям:
- система отрезков, удовлетворяющих условиям:
1) 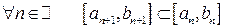 (система вложенных сегментов);
(система вложенных сегментов);
2) 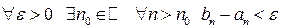 (стягивающаяся система отрезков).
(стягивающаяся система отрезков).
Тогда 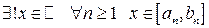 (т.е.
(т.е.  ).
).
Доказательство. Докажем существование элемента 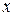 :
:  .
.
Пусть множество  состоит из левых концов сегментов
состоит из левых концов сегментов 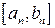 , т.е.
, т.е. 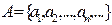 , а множество
, а множество  состоит из левых концов сегментов
состоит из левых концов сегментов 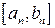 , т.е.
, т.е. 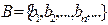 . Очевидно, что
. Очевидно, что  (из условия 1) теоремы). Тогда в силу свойства непрерывности множества действительных чисел
(из условия 1) теоремы). Тогда в силу свойства непрерывности множества действительных чисел 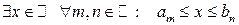 . В частности,
. В частности, 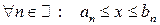 . Таким образом,
. Таким образом,  , т.е.
, т.е.  .
.
Докажем единственность элемента 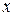 методом доказательства от противного. Предположим обратное, т.е. что
методом доказательства от противного. Предположим обратное, т.е. что 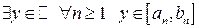 и
и  . Пусть, например,
. Пусть, например,  . Тогда
. Тогда 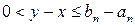 . Но по условию 2) теоремы
. Но по условию 2) теоремы 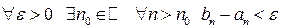 . Следовательно,
. Следовательно, 
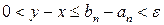 ,
,
В частности, при 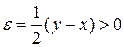 получаем, что
получаем, что 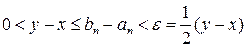 , откуда,
, откуда, 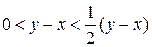 , что невозможно. Пришли к противоречию, а, следовательно, единственность элемента
, что невозможно. Пришли к противоречию, а, следовательно, единственность элемента 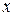 доказана. Теорема доказана.
доказана. Теорема доказана.
Замечание. Заметим, что для доказательства существования элемента 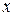 мы использовали только свойство 1) условия теоремы, т.е. то, что мы имеем систему вложенных сегментов, а для доказательства его единственности – свойство 2), т.е. то, что мы имеем стягивающуюся систему сегментов.
мы использовали только свойство 1) условия теоремы, т.е. то, что мы имеем систему вложенных сегментов, а для доказательства его единственности – свойство 2), т.е. то, что мы имеем стягивающуюся систему сегментов.
Теорема Кантора. Множество действительных чисел не является счётным, т.е.  .
.
Доказательство. Покажем, что любой отрезок  числовой прямой (
числовой прямой (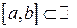 ) не является счётным множеством методом доказательства от противного.
) не является счётным множеством методом доказательства от противного.
Предположим противное, т.е. что отрезок  является счётным множеством, а значит, все его элементы можно занумеровать:
является счётным множеством, а значит, все его элементы можно занумеровать: 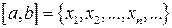 . Обозначим через
. Обозначим через 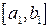 отрезок такой, что
отрезок такой, что 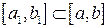 и
и 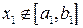 . Обозначим через
. Обозначим через  отрезок такой, что
отрезок такой, что  и
и  . Далее продолжаем этот процесс. На
. Далее продолжаем этот процесс. На 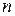 -ом шаге обозначим
-ом шаге обозначим 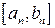 отрезок такой, что
отрезок такой, что 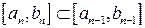 и
и 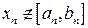 . Продолжая этот процесс далее, мы получим систему вложенных сегментов
. Продолжая этот процесс далее, мы получим систему вложенных сегментов 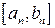 такую, что
такую, что 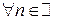
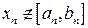 . По принципу Кантора вложенных сегментов
. По принципу Кантора вложенных сегментов  , а, следовательно,
, а, следовательно, 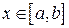 . Но все точки отрезка
. Но все точки отрезка  перенумерованы, т.е.
перенумерованы, т.е.  . Следовательно, мы получили, что
. Следовательно, мы получили, что
 ,
,
в частности,  , что невозможно в силу построения отрезков
, что невозможно в силу построения отрезков 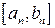 . Мы пришли к противоречию, тем самым доказав, что любой отрезок
. Мы пришли к противоречию, тем самым доказав, что любой отрезок  числовой прямой не является счётным множеством.
числовой прямой не является счётным множеством.
Далее, если бы множество действительных чисел  было счётным, то по лемме 2 любое его бесконечное подмножество, в частности, и любой отрезок, было бы счётным множеством, что противоречит уже доказанному. Теорема Кантора доказана.
было счётным, то по лемме 2 любое его бесконечное подмножество, в частности, и любой отрезок, было бы счётным множеством, что противоречит уже доказанному. Теорема Кантора доказана.
Поиск по сайту: