Числовые характеристики случайных величин

Закон распределения полностью характеризует случайную величину. Чтобы оп­ределить закон распределения случайной величины, достаточно задать ее плот­ность вероятности или функцию распределения. Однако, для решения многих практических задач достаточно знать лишь некоторые числа, характеризующие распределение, так называемые числовые характеристики случайной величины. Из числовых характеристик наиболее часто используются моменты случайной величины. Первый момент называется математическим ожиданием (или средним случайной величины) и вычисляется по одной из следующих формул (первая форму­ла применяется для дискретных случайных величин, а вторая — для непрерывных):

MX=∑x_ip_i MX=∫xf(x)dx

Величина MX характеризует среднее положение значений случайной вели­чины X.

Второй центральный момент характеризует разброс значений случайной величины вокруг зна­чения MX и называется дисперсией. Дисперсия DX (часто также используют обозначение σ² или σ_х²) вычисляется по формулам (первая формула применяется для дискретных случайных величин, а вторая — для непрерывных)

Равномерное непрерывное распределение. Непрерывная случайная величина ξ имеет равномерное распределение в интервале (a,b), если её функция плотности f(x) и распределения F(x) имеют вид:

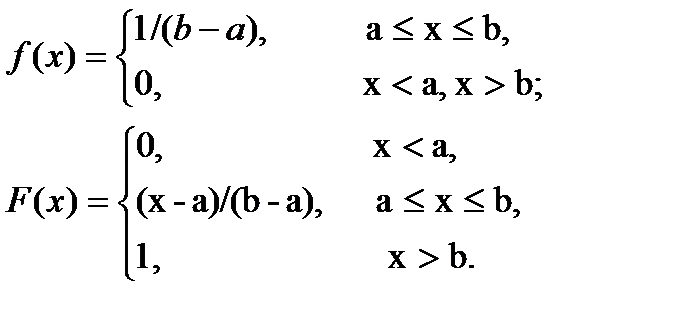
или графически

В этом случае числовые характеристики случайной величины ξ, принимающей значения x – математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно будут:

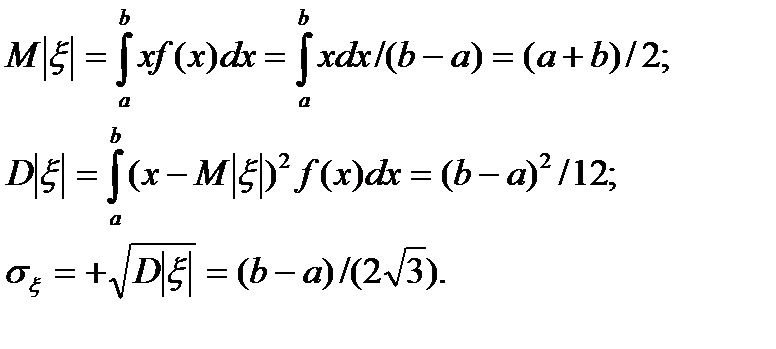
Если границы интервала a=0, b=1 то функции плотности и распределения имеют вид:

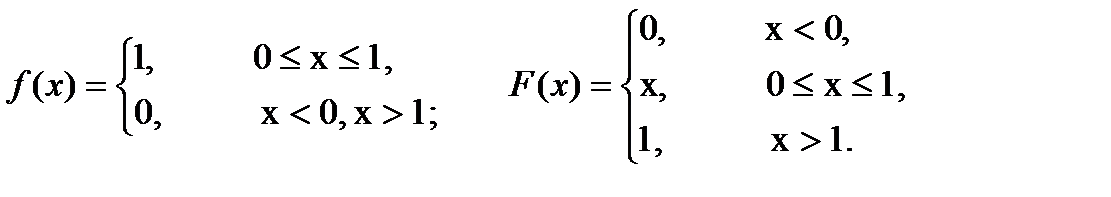
а математическое ожидание M|ζ| = 1/2 и дисперсия D|ζ| = 1/12. Получить это распределение на цифровой ЭВМ невозможно, так как машина оперирует с n-разрядными числами. По­этому на ЭВМ вместо непре­рывной совокупности равно­мерных случайных чисел ин­тервала (0, 1) используют дискретную последователь­ность 2n случайных чисел то­го же интервала. Закон рас­пределения такой дискрет­ной последовательности на­зывают квазиравномерным распределением.

Поиск по сайту: