 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Математическое ожидание и дисперсия квазиравномерной случайной величины имеют вид
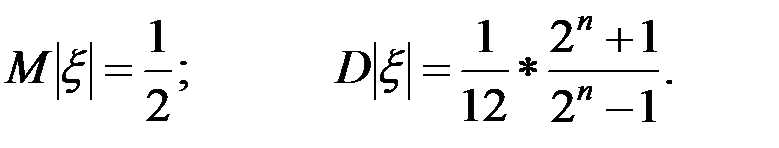
Дисперсия отличается от дисперсия равномерно распределенной случайной величины только множителем (2n+1)/(2n-1.
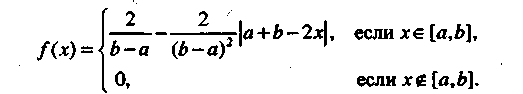
|
Треугольное распределение. Случайная величина X имеет треугольное распределение на интервале [а, b], если ее плотность вероятности вычисляется по формуле
Для этой случайной величины МХ = (4(а3+63)-(а+6)3)/ 6(b-a)2, DX = (b-a)3/24. Если Xt и Х2 — независимые случайные величины, равномерно распределенные на интервале [a/2, b/2], то случайная величина X = X1 + Х2 имеет треугольное распределение на интервале [а,b], представленное на рис. 1.1.
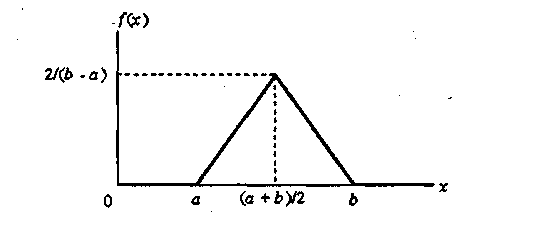
Рис. 1.1. Плотность треугольного распределения
Показательное (экспоненциальное) распределение. Случайная величина X имеет показательное (экспоненциальное) распределение с параметром λ(λ> 0), если ее плотность вероятности вычисляется по формуле
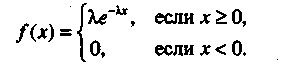
Для этой случайной величины MX = 1/ λ, DX = 1/ λ2; ее функция распределения вычисляется по простой формуле F(u) = 1 - еλu (u > 0). Эта распределение часто встречается в моделировании случайных процессов (оно обладает так называемым свойством отсутствия последействия), рис.1.2.
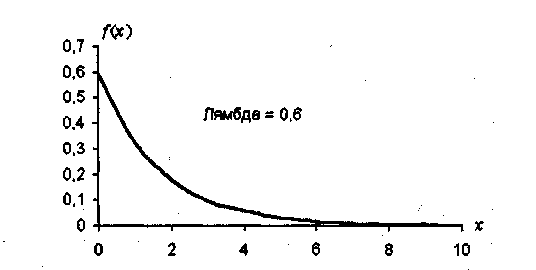
Рис.1.2. Плотность показательного распределения
Нормальное распределение. Случайная величина X имеет нормальное распределение с параметрами mи σ2, если ее плотность вероятности вычисляется по формуле

Для этой случайной величины MX = m, DX = σ2. Нормальное распределение называют также гауссовским распределением.
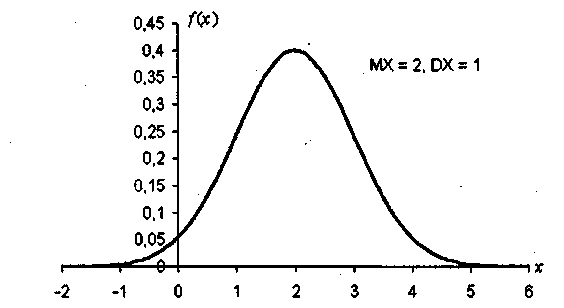
Если m=0 и σ2 = 1, то распределение называется стандартным нормальным распределением. Линейное преобразование Y = (X - m)/σ приводит произвольную нормально распределенную величину X к стандартному нормальному распределению, показанному на рис. 1.3.
Фундаментальная роль, которую играет нормальное распределение в теории вероятностей и математической статистике, объясняется тем, что при достаточно широких условиях распределение суммы случайных величин с ростом числа слагаемых асимптотически сходится к нормальному (центральная предельная теорема теории вероятностей).
|
Рис.1.3. Плотность нормального распределения
Нормально распределенная случайная величина с большой вероятностью принимает значения, близкие к своему математическому ожиданию.
На ЭВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений х случайной величины ζ используются формулы (алгоритмы). Поэтому такие последовательности, являющиеся по своей сути детерминированными, называются псевдослучайными.
Полученные с помощью генератора псевдослучайные последовательности чисел должны состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получаться с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.
Моделирование случайных величин с помощью компьютера основано на преобразовании случайных чисел, имеющих равномерное распределение на интервале [0, 1] в случайные величины, имеющие другие распределения.
Получение случайных чисел, имеющих равномерное распределение на интервале [0, 1] возможно различными способами.
Мультипликативный способ заключается в следующем: если ri = 0,0040353607, то ri+1 = {40353607·ri }mod 1, где mod 1 означает операцию извлечения из результата только дробной части после десятичной точки. Литературные источники говорят, что числа ri, начинают повторяться после цикла из 50 миллионов чисел, так что r50000001= ri. Последовательность ri получается квазиравномерно распределенной на интервале (0, 1). Однако, наиболее часто используются стандартную функцию, имеющуюся в языках программирования. Будем называть эту функцию random().
Проверкакачества последовательностей псевдослучайных чисел {xi } на соответствие закону распределения может быть выполнена с помощью гистограмм. Интервал (xmin, xmax) разбивается на т равных частей (подинтервалов), тогда при генерации последовательности { xi } каждое из чисел хj с вероятностью pj= 1/m, j= 1,2,…,m,попадает в один из подынтервалов.
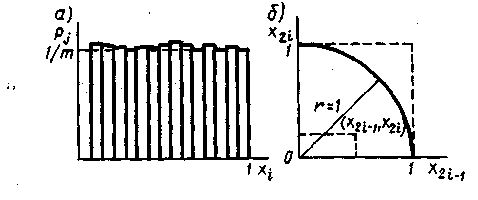
Построив столбики высота которых пропорциональна количеству значений xi, попавших в подинтервал, получим гистограмму наглядно представляющую распределение значений рассматриваемой величины.
Допустим, имеется n измерений некоторой величины х1, х2,..., хn. Для построения гистограммы выполним следующие действия.
1. Определим размах выборки х1, х2,..., хn, т.е. R = xmax - xmin
2. Интервал R делим на m равных участков (допустим  ), желательно, чтобы 5<= m <=20; тогда ширина одного участка s = r/m.
), желательно, чтобы 5<= m <=20; тогда ширина одного участка s = r/m.
3. Определим количество значений xi, попавшихв каждый из m участков. Для этого используем формулу для номера участка, в который попадает значение xi: k:=[(xi-xmin)/s]+1, где k -номер участка в который попадает значение xi, s -ширина одного участка, [ ] означают, что нужно взять целую часть значения в скобках. Учтем, что применение этой формулы для xmax дает k= m + 1.
4. Строим m столбцов равной ширины, высота столбцов пропорциональна количеству значений xi , попавшихв соответствующий участок интервала.
В результате вместо n чисел получим m чисел (m<<n).
Алгоритм решения этой задачи можно представить в следующем виде (рис. 1.4).
| Ввод исходных данных |
| Определение количества значений, попадающих в k-й участок |
| Генерирование случайных значений |
| начало |
| i=1, n |
| Xi=случ.знач |
| Определение Xmax и Xmin R= Xmax - Xmin S = R/5 |
| i=1, n |
| k=[(Xi-Xmin)/S]+1 Yk=Yk+1 |
| Построение гистограммы: столбики высотой Y1,Y2,Y3,Y4,Y5 |
| конец |
Рис.1.4. Схема алгоритма получения случайных чисел и построения гистограммы их распределения (m =5).
Рассмотрим некоторые способы преобразования последовательности равномерно распределенных случайных чисел {х,} в последовательность с заданным законом распределения {yj}
Формула, используемая для создания генератора случайных чисел равномерно распределенных на интервале (a, b), использующая функцию random(), имеет следующий вид:
a + (b - а)* random().
Формулы для создания генераторов случайных чисел:
- длясимметричного треугольного распределения:
a + (b - а)*(random()+random())/2;
- для нормального распределений имеющего среднее значение μ, (соответствующее максимальной вероятности) и среднеквадратическое отклонение σ, (определяющее ширину или размах распределения) числа an можно получить с помощью алгоритма:
a:=0.0;
for i=1 to 12 do a:= a + random()
an:= μ + (a-6.0)* σ;
- псевдослучайную последовательность, распределенную по экспоненциальному закону можно получить с помощью алгоритма:
r:= log(random());
me:= μ *(-r); μ – математическое ожидание.
Задание.
1. Изучить теоретический материал.
2. Написать программу, реализующую алгоритм получения случайных чисел и построения гистограммы их распределения (гистограмму можно строить в Excel, для чего получаемые случайные величины выводить в лист Excel).
3. Реализовать программное получение последовательности случайной величины:
а) равномерно распределенной на заданном интервале,
б) для симметричного треугольного распределения,
в) для нормального распределения,
г) для экспоненциального распределения.
4. С помощью гистограмм проанализировать влияние количества значений (n) на качество получаемых последовательностей.
5. Рассмотреть распределение случайных величин для нескольких вариантов размера выборки (20, 100, 300 значений).
6. Представить полученные результаты преподавателю.
7. Подготовить ответы на контрольные вопросы.
Чем вызвана необходимость генерации случайных величин в имитационном моделировании?
Как можно оценить качество псевдослучайных чисел, получаемых с помощью стандартной функции языка программирования random()?
Какие исходные данные нужны для получения случайных чисел имеющих нормальное распределение, экспоненциальное распределение, симметричное треугольное распределение?
Поиск по сайту: