АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Генеральная и выборочная дисперсия. Групповая, внутригрупповая, межгрупповая и общая дисперсии

Читайте также:
  1. I. Раздел общая дерматология.
  2. III. Общая ответственность за вред
  3. Билет №10. Пищевая промышленность. Общая хар-ка отрасли. Влияние на ОС.
  4. Биноминальная случайная величина, ее мат. ожидание и дисперсия. Случаи применения этой случайной величины.
  5. Блок 4- Общая и молекулярная генетика
  6. Блок 4- Общая и молекулярная генетика
  7. Блок 4- Общая и молекулярная генетика
  8. В 1. Перенос расплавленного металла в сварочной дуге. Силы, действующие в дуге на расплавленный металл, общая характеристика.
  9. В-7 Общая характеристика первобытного общества?
  10. Вопрос 9. Устав уголовного судопроизводства 1864 г.: общая характеристика и значение для развития российского уголовного процесса.
  11. Генеральная и выборочная совокупности.

 

для того чтобы охарактизировать рассеяние значений количественного признака Х гене-ральной совокупности вокруг своего среднего значения вводят сводную характеристику –генеральную дипресию. Генеральной дипресией называют среднее арифметическое квадратов отклонения значений признака генеральной совокупности от их среднего значения. Если все значения признака генеральной совокупности объема N различны,то если же значения при-знака имеет соответственно частоты причем + то т.е. генеральная дис-персия есть средняя взвешенная квадратов от-клонения с весами, равными соответствующим частотам. Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением. Генеральным средним квадратическим отклонением (стандар-том) называют квадратный корень из генераль-ной дипресии:

Выборочная дисперсия

Для того чтобы охарактизировать рассеяние наблюдаемых значений количественного при-знака выборки вокруг своего среднего значения вводят сводную характеристику –выборочную дисперсию. Выборочной дисперсией называ-ют среднее арифметическое квадратов отклоне-ния наблюдаемых значений признака от их сред-него значения если все значения признака выборки объема nразличны, то если же значения признака имеет соответственно час-тоты причем т.е. выборочная дис-персия есть средняя взвешаная квадратов откло-нения с весами, равными соответствующим частотам. Кроме дисперсии для характеристики рассеяния значений признака выборочной сово-купности вокруг своего среднего значения поль-зуются сводной характеристикой – средним квадратическим отклонением. Выборочным средним квадратическим отклонением (стандар-том) называют квадратный корень из выбороч-ной дисперсии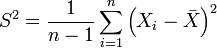

 

Общая дисперсия оценивает колеблемость признака всех единиц совокупности без исключения:

 

 

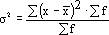
– средняя в целом по совокупности;

 

f – частота в целом по совокупности.

 

Она отражает влияние всех причин и факторов, которые действуют на вариацию.

 

Для характеристики вариации признаков по группе рассчитывают групповую дисперсию. Она рассчитывает колеблемость признака в каждой отдельной группе и представляет собой средний квадрат отклонений индивидуальных значений признаков от средней по каждой отдельно взятой группе: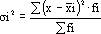

Межгрупповая дисперсия (дисперсия групповых средних) характеризует вариацию результативного признака под влиянием только одного фактора, положенного в равновесие группировки


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)