АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Статистические характеристики систем случайных величин

Читайте также:
  1. B. Взаимодействие с бензодиазепиновыми рецепторами, вызывающее активацию ГАМК – ергической системы
  2. C. Обладать незначительной системной биодоступностью
  3. CRM системы и их возможности
  4. D) по 20 бальной системе
  5. I ступень – объектив- центрическая система из 4-10 линз для непосредственного рассмотрения объекта и формирования промежуточного изображения, расположенного перед окуляром.
  6. II. Освоение техники микроскопии с иммерсионной системой.
  7. II. Світовий освітній простір і система освіти в Україні.
  8. III. Физиология специфических сенсорных систем
  9. IV. Настільні видавничі системи.
  10. IV. Поземельные книги и другие системы оглашений (вотчинная и крепостная системы)
  11. V. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ЗНАНЬ
  12. VI. Система органов дыхания

Характеристики случайных величин

 

Математическое ожидание.

 

Свойства математического ожидания.

 

Дисперсия. Свойства дисперсии.

 

Среднее квадратичное отклонение.

Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.

Свойство 1. Математическое ожидание постоянной равно самой этой постоянной.

 

Постоянная С принимает это значение с вероятностью единица и по определению М(С)=С×1=С

 

Свойство 2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Свойства дисперсии.

 

Свойство 1. Дисперсия постоянной равна нулю.

Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.

Свойство 3. Если случайные величины Х и У независимы, то

часто предпочитают пользоваться другой характеристикой разброса – средним квадратическим отклонением, которое равно корню квадратному из дисперсии.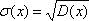

Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

Статистические характеристики систем случайных величин.

статистические характеристики случайных величин:

мода, медиана, среднее выборочное значение

Мо́да — значение во множестве наблюдений, которое встречается наиболее часто. Случайная величина может не иметь моды. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9).

Медиа́на (50-й перцентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)