Статистические оценки параметров распределения. Генеральная и выборочная средние. Групповая и общая средние

Пусть требуется изучить некоторый количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак и необходимо оценить параметры, которыми оно определяется. Например, если изучаемый признак распределен в генеральной совокупности нормально, то нужно оценить математическое ожидание и среднее квадратическое отклонение; если признак имеет распределение Пуассона – то необходимо оценить параметр λ.

Для того чтобы статистические оценки давали корректные приближения оцениваемых параметров, они должны удовлетворять некоторым требованиям, среди которых важнейшими являются требования несмещенности и состоятельности оценки. Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам.

Эффективной называют статистическую оценку, которая, при заданном объеме выборки n, имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называется статистическая оценка, которая при n→∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n→∞ стремится к нулю, то такая оценка оказывается и состоятельной.

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.

Точечной оценкой генеральной средней является выборочное среднее.

Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0).

Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.

Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной.

Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.

Если все значения x1, x2,..., xn признака выборки объема n различны, то: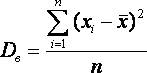

Групповой средней называют среднее арифметическое значений признака, принадлежащих группе

Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней

Поиск по сайту: