ГЕОМЕТРИЧЕСКИЕ МОДЕЛИ ДВОИЧНОГО КОДА

ВЗАИМОДЕЙСТВИЕ СИГНАЛОВ И ПОМЕХ

· Внешние и внутренние помехи взаимодействуют с сигналами внутри схемы информационных устройств, внешние помехи (наводки) кроме того - с сигналами, передаваемыми по каналам связи к приёмным полукомплектам устройств.

Реальный характер поведения помех без проведения специальных статистических исследований считают соответствующим версии «белого шума». Воздействие помех вызывает искажения сигналов в процессе их передачи и преобразования. В кодированных сигналах могут возникать ошибки, связанные с изменением отдельных символов в кодовых словах - ошибки воспроизведения 0 ® 1 или стирания 1 ® 0. Характерные свойства взаимодействия сигнала и помехи:

- вероятность ошибки в любой позиции сообщений (сигналов) одинакова;

- ошибки в различных позициях сообщений (сигналов) независимы.

ГЕОМЕТРИЧЕСКИЕ МОДЕЛИ ДВОИЧНОГО КОДА

· Кодовые n- разрядныекомбинации (кодовые слова) – последовательности разрядных коэффициентов числа или кортежи с длиной n. Согласно представлению кортежей векторами n- мерногопространства, геометрическую модель n-разрядного НДК изображают в виде n-мерного куба (гиперкуба), множество вершин которого определяет положение векторов-кортежей

кодо 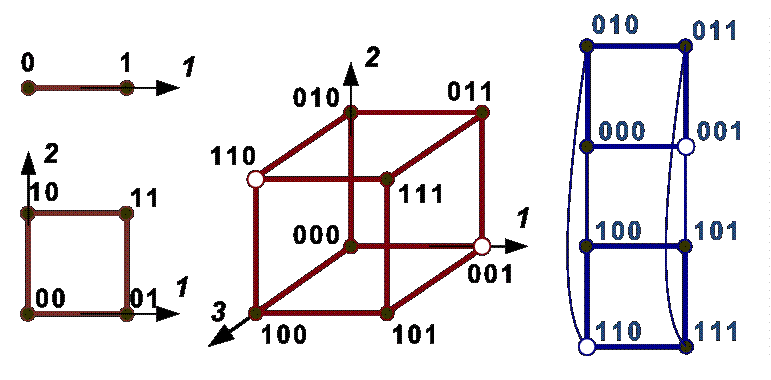вых слов. Координатные оси гиперкуба соответствуют разря-дам кода, а коэффициенты a_i – координатам точек по i -ой оси. У одноразрядного двоичного кода гиперкуб модели вырождается в линию, у двухразрядного – в плоский квадрат, а у трехразрядного – становится обычным трёхмерным кубом (см. геометрические модели НДК).

· Переход от одной кодовой комбинации к соседней, например, от 010 к 011, называется кодовым переходом. Смещение на один кодовый переход сопровождается изменением одного символа в исходной комбинации. Расстояние d между любыми двумя кодовыми комбинациями, определяемое наименьшим числом переходов по линиям куба, называют кодовым расстоянием (расстоянием Хэмминга). Кодовое расстояние можно определить как число единиц («1») в результате полусложения (сложения по модулю 2) коэффициентов разрядов кодовых слов.

· Объёмную модель НДК трудно изобразить при n ³ 3. В этом случае используют плоскостные модели в виде графов. Для построения графа n -элементного g -ричного кода следует:

- построить модель n-1 -элементного g -ричного кода;

- изобразить на расстоянии одного кодового перехода g-1 зеркальных отображений этой модели;

- добавить у кодовых комбинаций основной модели на старших n -ых позициях символы 0, а у зеркальных моделей – символы от 1 до g-1;

- соединить комбинации, находящиеся на расстоянии d=1.

· Из геометрических моделей НДК видно, что минимальное кодовое расстояние между комбинациями равно одному кодовому переходу

и любая ошибка вида 0 ® 1 или 1 ® 0 преобразует одно кодовое слово в другое, т.е. приведёт к искажению информации. Из этого следует, что использование для передачи всех возможных кодовых комбинаций делает код безизбыточным, но совершенно не защищённым от помех. Это относится и к разновидностям НДК, и к двоично-десятичному коду, и к коду Грея.

· Коды, позволяющие обнаружить или исправить ошибки, называют помехозащищёнными. Общий подход к обеспечению помехоустойчивости кодов сводится к введению в них избыточности – добавлению в исходные комбинации служебных (контрольных) символов. Это позволит, выполнив специальные проверки принятого кода, сформировать опознаватель наличия ошибки, и даже искажённого разряда.

· С добавлением контрольных символов увеличиваются длина кодовых комбинаций и общее их количество. Необходимое число слов, которые считаются разрешёнными, отбирается для передачи, а остальные переводятся в категорию запрещённых.

Пример. В 3-разрядном НДК (см. таблицу) можно выбрать в качестве разрешённых кодовые слова 1, 4, 6 и 7 с чётным числом единиц В любой паре выбранные слова отличаются значениями двух разрядов, следовательно, все они разделены кодовым расстоянием d=2. Одиночная ошибка переводит разрешённое слово в одно из запрещённых, отстоящее на d=1. Каждому разрешённому слову соответствует одна из множеств А, С, Д и Е запрещённых комбинаций с нечётным числом единиц. Ошибка можно выявить подсчётом числа единиц в принятой комбинации.

Четыре разрешённых слова c n=3 соответствуют общему количеству слов в безизбыточном двухразрядном НДК – N=2ⁿ=2²=4. Первые два разряда в каждом слове – информационные (m=2). Избыточность кода свидетельствует, что один из трёх разрядов – контрольный (k=1).

· Технически подобные коды составляют добавлением к m информационным разрядам одного контрольного разряда справа (структура n=m + 1). Контрольный разряд формируется как результат полусложения единиц в информационных разрядах. Тогда общее число единиц в каждом слове окажется чётным, а сформированный код называют кодом с проверкой на чётность. Ошибка выявляется полусложением всех единиц принятого слова. Единичный результат полусложения, укажет наличие искажения (опознаватель ошибки).

Соответственно можно построить код с проверкой на нечётность. Для обоих кодов необходимое кодовое расстояние – d=r + 1=2,

где r=1 – число обнаруживаемых ошибок. Их относят к помехозащищённым кодам с обнаружением одиночной ошибки, хотя они позволяют в принципе обнаружить любое нечётное число ошибок.

· Возможность исправления ошибки достигается увеличением избыточности кода.

Обнаружить наличие одиночной ошибки в рассмотренном примере с 3-раз­рядным НДК позволил выбор в качестве разрешённых слов тех, которые находятся на кодовом расстоянии d=2. Для возможности исправления ошибки требуется увеличить избыточность, поэтому отберём из 3-разрядного НДК комбинации на расстоянии d= 3. Этому условию удовлетворяет несколько разных пар. Выберем в качестве разрещённых кодовые слова 2 и 7(001 Å 110=111). Для передачи двух сообще-

ний достаточ но одноразрядного НДК (m = 1). Поэтому избыточность кодовых слов

i= (n–m) /n= (3–1) /3=2/3,

а число контрольных символов k=2.

Одиночная ошибка переведёт слово 2 в одно из запрещённых слов множества В, а слово 7 – в одно из слов множества Е. Эти непересекающиеся мно­жества В и Е называют подгруппами декодирования разрешённых кодовых слов. Они позволяют исправить одиночную ошибку, так как фиксация на приёме любого слова из этих подгрупп считается эквивалентной приёму ближайшего разрешённого слова (декодирование по методу максимального правдоподобия).

d ≥ 2s + 1.

В общем случае, для исправления s и обнаружения r ошибок (дополнительно) требуется обеспечить кодовое расстояние

d ≥ r + 2s + 1.

Следует отметить, что корректирующие коды предназначаются для исправления ошибок (или их комбинаций), наиболее вероятных для конкретного канала. Они не гарантируют безошибочного приёма любого искаженного слова, поскольку реально может встретиться бóлее сложная комбинация ошибок (хотя и очень редко). Но, в целом, применение корректирующих кодов значительно повышает вероятность правильного приёма информации.

Поиск по сайту: