АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Множество Кантора

Читайте также:
  1. Множество инвестиционных возможностей
  2. Множество инвестиционных возможностей при наличии безрисковой доходности
  3. Множество людей ошибочно полагают, что, принимая наркотики, они находятся на пути к высокой духовности.
  4. Таким же образом вы можете нарисовать себе множество различных веселых картинок.
  5. Тесноту линейной корреляционной связи между одной случайной величиной и некоторым множеством случайных величин.

 

Канторово множество - один из простейших фракталов. Это подмножество единичного отрезка вещественной прямой, которое является классическим примером «плохого множества» в математическом анализе. Описано в 1883 году Георгом Кантором.

Построение

Из единичного отрезка удалим среднюю треть, т.е. интервал (). Оставшееся точечное множество обозначим через . Множество состоит из двух отрезков. Удалим теперь из каждого отрезка среднюю треть, и оставшиеся множества обозначим как . Повторим эту процедуру снова. Удаляя средние трети у каждого из четырех получившихся отрезков, получим множество . Дальше таким же образом получаем ... Теперь обозначим через пересечение всех . Множество будет называться Канторовым множеством.

 

Свойства

• Канторово множество не счетное

• Канторово множество имеет промежуточную Хаусдорфову размерность равную

 

 

Рисунок 3. Множество Кантора на 7-ой итерации


Ковер Серпинского

 

Ковер Серпинского (квадрат Серпинского) – фрактал, являющийся одним из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским.

Построение

Квадрат 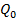делится прямыми, параллельными его сторонам, на 9 равных квадратов. Из квадрата 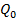удаляется центральный квадрат. Получается множество, состоящее из восьми оставшихся квадратов «первого ранга». Повторяя процедуру для каждого из квадратов первого ранга, получим множество , состоящее из 64 квадратов «второго ранга». Продолжая этот процесс бесконечно, получим бесконечную последовательность

,

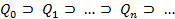пересечение членов которой и есть Ковер Серпинского.

Свойства

• Ковер Серпинского имеет промежуточную Хаусдорфову размерность

 

 

Рисунок 4. Ковер Серпинского на 6 итерации


 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (1.43 сек.)