Фізичний маятник

Реферат

на тему:

«Механічні коливання»

Виконав:____________

__________________________

МЕХАНІЧНІ КОЛИВАННЯ І ХВИЛІ

Коливання – це рухи або процеси, які повторюються у часі.

Залежно від фізичної природи коливання поділяються на:

· механічні,

· електричні,

· електромеханічні,

· електромагнітні,

· акустичні.

Залежно від зовнішньої дії коливання можуть бути:

· вільними – здійснюються за рахунок енерґії, що була початково надана системі,

· вимушеними – здійснюються за рахунок енерґії, яку система одержує в процесі руху

Характеристики гармонічних коливань

Коливання називаються гармонічними якщо величина, що коливається, змінюється в часі за косинусоїдальним (синусоїдальним) законом:

φ₀); (3.1)

швидкість:

φ₀) φ₀); (3.1а)

прискорення:

φ₀) φ₀) (3.1б)

x – зміщення – відхилення тіла від положення рівноваги;
А – амплітуда коливань – найбільше відхилення тіла від

положення рівноваги;

φ 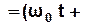φ₀) - фаза коливань, визначає положення тіла у

момент часу t;

φ₀ -початкова фаза коливань, визначає положення тіла у момент

часу t = 0;

- власна циклічна частота;

Т – період – час здійснення одного повного коливання.

Зв’язок між періодом і власною циклічною частотою коливань має вигляд:

. (3.2)

Пружинний маятник

Пружинний маятник – це тверде тіло, підвішене на абсолютно пружній невагомій пружині, яке під дією пружної сили може здійснювати гармонічні коливання.

Якщо тіло висить нерухомо (рис.3.1Б), то пружина видовжена на x_ст (статичний розтяг) порівняно з ненавантаженою пружиною (рис.3.1А), а умова рівноваги тіла запишеться у вигляді:

, (3.3)

де - kx_ст = F_ст (k – коефіцієнт жорсткості пружини).

(3.4)

і другий закон Ньютона запишеться у вигляді:

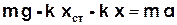. (3.5)

Врахувавши (3.3), рівняння (3.5) подамо у вигляді:

= , або (3.6) > 0, тому можна представити 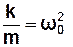. (3.7)

З врахуванням (3.7) рівняння (3.6) прийме вигляд:

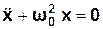. (3.8)

Розв’язок (3.8) є рівнянням гармонічних коливань:

φ₀) (3.9)

Період коливань визначаються масою тіла і жорсткістю пружини:

. (3.10)

Фізичний маятник

Фізичний маятник - це тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить через центр маси тіла.

При відхиленні маятника від положення рівноваги на кут a виникає обертальний момент (рис.3.2):

, (3.11)

де - складова сили тяжіння яка повертає

маятник у положення рівноваги.

Використавши рівняння динаміки обертального руху твердого тіла:

, (3.12)

де J₀ – момент інерції маятника відносно осі, що проходить

через точку О;

- кутове прискорення маятника

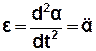, (3.13)

одержимо:

, (3.14)

або: 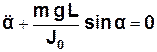(3.15)

Позначивши: , (3.16)

одержуємо диференціальне рівняння коливань маятника:

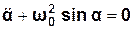. (3.17)

Якщо кут відхилення малий (), то ; рівняння (3.17) набуде вигляду:

. (3.18)

і його розв’язком є рівняння гармонічних коливань:

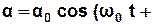φ₀), (3.19)

де - максимальний кут відхилення;

Період коливань фізичного маятника:

. (3.20)

Позначимо: 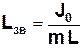, тоді . (3.21)

Зведена довжина фізичного маятника L_зв – це довжина такого математичного маятника, період коливань якого співпадає з періодом коливань даного фізичного маятника.

Оборотний маятник – це фізичний маятник, який має дві осі обертання, паралельні одна одній (О та О^’). Ці осі знаходяться на віддалі L_зв. Точка О^’ називається центром гойдання. Точка підвісу О і центр гойдання О^’ мають властивість взаємозамінності: при перенесенні точки підвісу у центр гойдання О^’ попередня точка підвісу О стане новим центром гойдання. Період коливань при цьому не зміниться.

Поиск по сайту: