Крутильний маятник

Крутильний маятник – це тверде тіло, закріплене на жорсткій підвісці, яке може здійснювати крутильні коливання під дією сил пружності деформації кручення підвіски.

При закручуванні маятника на кут виникає момент пружної сили, який намагається повернути маятник у положення рівноваги

M = - f , (3.24)

і пружних властивостей матеріалу дротини.

Оскільки після закручування маятник буде здійснювати обертальний рух навколо своєї вертикальної осі, яка проходить через точку підвісу вздовж дротини, то:

M = J ,(3.25)

де J – момент інерції маятника відносно осі закручування.

Врахувавши (3.13), (3.24), рівняння (3.25) запишемо у вигляді:

, (3.26)

або:

. (3.27)

Ввівши позначення:

, (3.28)

отримаємо диференціальне рівняння гармонічних коливань крутильного маятника:

. (3.29)

Розв’язком (3.28) є рівняння гармонічних коливань:

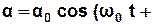φ₀). (3.30)

Період коливань крутильного маятника:

. (3.31)

7. Згасаючі коливання

Реальні механічні коливання здійснюються при наявності сил опору середовища. Тому механічна енерґія коливної системи з часом зменшується, а самі коливання загасають. Сила опору середовища переважно пропорційна швидкості руху тіла, що здійснює коливання:

, (3.32)

де r – коефіцієнт опору середовища,

знак (-) вказує на протилежний напрям сили опору

і швидкості руху.

Нехай тіло масою m під дією пружної сили -kx і сили опору здійснює коливання вздовж осі OX. Рівняння руху такого тіла:

, (3.33)

або: . (3.34)

Позначивши:

; ,

де - коефіцієнт згасання,

запишемо диференціальне рівняння згасаючих коливань:

. (3.35)

Якщо > , розв’язком (3.35) є рівняння:

φ₀), (3.36)

яке описує гармонічні коливання з циклічною частотою і змінною у часі амплітудою при початко-

вій амплітуді А₀ (рис.3.4)

Період згасаючих коливань: . (3.37)

· Декрементом згасання D називається відношення амплітуд двох послідовних коливань:

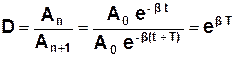. (3.38)

· Лоґарифмічним декрементом згасання називається фізична величина:

. (3.39)

· Часом релаксації коливальної системи називається проміжок часу протягом якого амплітуда коливань зменшується в е разів (е – основа натурального лоґарифму)

· Коефіцієнтом згасання називається фізична величина, обернена до часу релаксації:

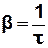. (3.40)

· N_е – число коливань, після здійснення яких амплітуда зменшується в е разів, так що = N_еT.

= Т = . (3.41)

Отже лоґарифмічний декремент згасання - це фізична величина, обернена до числа коливань N_e, після здійснення яких амплітуда зменшується в е разів.

· Добротністю системи називається фізична величина:

,(3.42)

де Е – енерґія системи у даний момент часу;

E – енерґія, втрачена протягом одного періоду.

Отже добротність системи тим більша, чим менші втрати

енерґії системи E. Можна показати, що:

= N_e. (3.43)

Поиск по сайту: