 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Построение схемы кодера и решетчатой диаграммы
КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ
Теоретические вопросы выбора оптимальных параметров и синтеза кодовых комбинаций сверточного кода рассмотрены в [1,2,5].
Кодер двоичного сверточного кода (СК) содержит регистр сдвигов на К разрядов и сумматоры по модулю 2 для образования кодовых символов. Входы сумматоров определены разрядами регистра. Связи i -го сумматора с ячейками j- го
-
Сверточные коды обычно задаются полиномами в восьмеричной системе счисления, и для построения схемы кодера необходимо перевести полиномы в двоичную (полиномиальную) форму.
Рассмотрим простейший несистематический код (7, 5). Для получения образующих полиномов переведем цифры в двоичную и полиномиальную формы:
G (1) =78 = 1112 ® D 2 + D + 1,
G (2) =58 = 1012 ® D 2 + 1.
 |
Схема кодера, соответствующая полиномам G (1) и G (2), приведена на рис. 2. На рисунке 3 показана описывающая его диаграмма состояний.
Сверточный кодер как конечный автомат с памятью описывают диаграммой состояний. Внутренними состояниями кодера считают символы, содержащиеся в (К – 1) разрядах регистра (начиная от входа кодера). Кодер на рис. 2 может находиться в одном из четырех состояний S 1 S 2 = (00, 10, 11, 01), так как К = 3. Диаграмма представляет собой направленный граф, который содержит все состояния и описывает возможные переходы из одного состояния в другое, а также символы входов/выходов кодера, сопровождающие эти переходы. В кружках указаны состояния кодера, стрелками – возможные переходы. Около стрелок показаны символы на входе/выходе кодера u/v (1) v (2), соответствующие каждому переходу.
Развертка диаграммы состояний во времени образует решетчатую диаграмму (рис. 4). На решетке состояния показаны узлами, а переходы – соединяющими их линиями (ветвями). После каждого перехода из одного состояния в другое происходит смещение на один шаг вправо. Решетчатая диаграмма представляет все разрешенные пути, по которым может продвигаться кодер при кодировании.

Рисунок 4
Свободное кодовое расстояние df СК определяется числом символов, которыми отличаются все возможные кодовые последовательности, при условии, что им соответствуют две последовательности, имеющие отличие в одном символе. Поскольку СК являются линейными, то в качестве одной последовательности удобно взять нулевую, а в качестве второй – последовательность с одной единицей на первом месте. В этом случае определение df упрощается, так как можно воспользоваться выражением
df = Wt (hi) (8)
где Wt (hi)– вес отклика (импульсной реакции) кодера на единичное воздействие вида
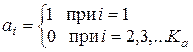 .
.
Рассчитаем свободное кодовое расстояние, исходя из решетчатой диаграммы кода, выбирая путь наименьшего веса, начинающийся и заканчивающийся в состоянии 00 (и отличный от нуля). На рис. 4 этот путь обозначен пунктирной стрелкой. Вес этого пути и будет свободным расстоянием кода df = Wt (11 10 11) = 5.
Поиск по сайту: