АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Для характеристик гиперболы определённых выше подчиняются следующим соотношениям

Читайте также:
  1. V. Характеристика современного гражданского права
  2. Автоматизированное рабочее место (АРМ) таможенного инспектора. Назначение, основные характеристики АРМ. Назначение подсистемы «банк - клиент» в АИСТ-РТ-21.
  3. Анализ возможных мест утечки веществ и характеристика этих веществ.
  4. Базовые стратегии конкуренции: характеристики, отличительные черты
  5. Бактерии, их характеристика
  6. Билет №6.Типы культуры,их характеристика
  7. В 1. Перенос расплавленного металла в сварочной дуге. Силы, действующие в дуге на расплавленный металл, общая характеристика.
  8. В 4. Вибрация, физические характеристики, нормирование и действие на организм человека. Виды средства защиты от вибрации.
  9. В 4. Виды производственного освещения и их характеристика. Основные светотехнические величины и единицы их измерения, КЕО.
  10. В 4. Виды производственного освещения и их характеристика. Основные светотехнические величины и единицы их измерения. КЕО
  11. В 4. Характеристика процесса горения. Виды горения. Горючие вещества Взрывопожароопасные свойства ГВ.
  12. В-7 Общая характеристика первобытного общества?

· .

· .

· .

· .

· .

· .

· .

· .

 

 

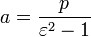· Гиперболу, у которой 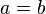, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a).

 

 

· Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:

,

где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению

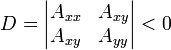
и

 

 

  • Канонический вид

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду

,

где a и b — полуоси

 

· Асимптоты

Для гиперболы, заданной в каноническом виде

уравнения двух асимптот имеют вид:

.

 

· Диаметры и хорды

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент соответствующего диаметра связан соотношением

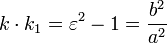
Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

 

· Применения

· Семейство конфокальных (софокусных) гипербол вместе с семейством софокусных эллипсов образуют двумернуюэллиптическую систему координат

.

· Другие ортогональные двумерные координатные системы, построенные с помощью гипербол, могут быть получены с помощью других конформных преобразований. Например, преобразование w = z ² отображает декартовы координаты в два семейства ортогональных гипербол.

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)