АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Через директрису и фокус

Читайте также:
  1. C. Через 10 – 30 мин и длится 1 – 2 часа
  2. А) конструкцію товару, фокусування на одному або кількох товарах
  3. Акцизы: налогоплательщики и объекты налогообложения. Особенности определения налоговой базы при перемещении подакцизных товаров через таможенную границу РФ.
  4. Взаимодействие через СМЭВ
  5. Вивчення процесів витікання рідини через отвори.
  6. Визначте рядок, у якому всі слова пишуться через дефіс
  7. Висвітлення прав дитини через засоби масової інформації
  8. Витікання рідини через водозлив.
  9. Витікання рідини через отвори
  10. Витікання рідини через отвори і насадки під рівень при постійному напорі
  11. Влияние через внушение
  12. Время — это горизонтальное измерение жизни, поверхностный слой реальности. Но еще есть вертикальное измерение глубины, доступ к которой пролегает через настоящий момент.

Коническое сечение

Гипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.

Как геометрическое место точек:

Через фокусы

Гипербола может быть определена, как Геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.

Для сравнения: кривая постоянной суммы расстояний между двумя точками — эллипс, постоянного отношения —окружность Аполлония, постоянного произведения — овал Кассини.

Через директрису и фокус

Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная называется эксцентриситетом гиперболы.

 

· Гипербола состоит из двух отдельных кривых, которые называют ветвями.

· Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.

· Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.

· Середина большой оси называется центром гиперболы.

· Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.

· Обычно обозначается a.

· Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.

· Обычно обозначается c.

· Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.

· Прямая, перпендикулярная действительной оси и проходящая через её центр называется мнимой или сопряженной осью гиперболы.

· Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.

· Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.

· Обычно обозначается b.

· В задачах, связанных с движением тел по гиперболическим траекториям расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием

· Обычно обозначается ..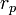

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)