Криптостойкость

Описанный выше метод шифрования обладает существен­ным недостатком. Если известна хотя бы часть исходного сообщения, то все сообщение может быть легко дешифровано. Действительно, пусть известно одно исходное словo . Тогда

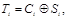
и далее вся правая часть гаммы шифра определяется по указанной формуле дат­чика псевдослучайных чисел.

На практике часть сообщения вполне может быть известна злоумышленнику. Например, многие текстовые редакторы помещают в начало файла документа одну и ту же служеб­ную информацию. Если злоумышленнику известно, что исходное сообщение подготовле­но в данном редакторе, то он сможет легко дешифровать сообщение.

Для повышения криптостойкости симметричных шифров применяют различные приемы:

1. Вычисление гаммы шифра по ключу более сложным (или секретным) спосо­бом;

2. Применение вместо более сложной (но обратимой) операции для вычисле­ния шифровки;

3. Предварительное перемешивание битов исходного сообщения по фиксирован­ному алгоритму.

Наиболее надежным симметричным шифром считается DES (Data Encryption Standard), в котором используется сразу несколько методов повышения криптостойкости.

В настоящее время широкое распространение получили шифры с открытым ключом. Эти шифры не являются симметричными — для зашифровки и расши­фровки используются разные ключи. При этом ключ, используемый для заши­фровки, является открытым (не секретным) и может быть сообщен всем жела­ющим отправить шифрованное сообщение, а ключ, используемый для расши­фровки, является закрытым и хранится в секрете получателем шифрованных сообщений. Даже знание всего зашифрованного сообщения и открытого ключа, с помощью которого оно было зашифровано, не позволяет дешифровать сообще­ние (без знания закрытого ключа).

Для описания метода шифрования с открытым ключом нужны некоторые факты из теории чисел, изложенные (без доказательств) далее.

Модулярная арифметика

Полагаем, что все числа целые. Говорят, что число а сравнимо по модулю п с числом b (обозначение: а b (mod n)), если а и b при делении на n дают один и тот же остаток:

а b (mod п) 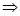a mod п = b mod n.

Отношение сравнимости рефлексивно, симметрично и транзитивно и является отношением эквивалентности. Классы эквивалентности по отношению сравни­мости (по модулю ) называются вычетами (по модулю п). Множество вычетов по модулю n обозначается Z _n. Обычно из каждого вычета выбирают одного пред­ставителя — неотрицательное число, которое при делении на n дает частное 0. Это позволяет считать, что Z _n = {0,1,2,... ,п — 1}, и упростить обозначения. Над вычетами (по модулю п) определены операции сложения и умножения по модулю n, обозначаемые, соответственно, + _n и 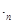и определяемые следующим образом:

а+_п b = (а + b) mod n, a 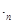b= mod n.

Здесь подразумеваются операции по модулю n, то индекс п опус­кается.

Легко видеть, что 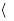Z _n; +_п 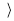образует абелеву группу, a 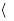Z _n; +_п ,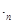 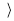— коммутатив­ное кольцо с единицей.

Рассмотрим Z^* _n — подмножество Z _n,чисел, взаимно простых с n. Числа а и b называются взаимно простыми, если их наибольший общий делитель равен 1. Можно показать, что 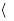Z _n^*; ^. _п 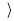— абелева группа. Таким образом, для чисел из множества Z _n^* Z^ существуют обратные по умножению по модулю n. Если n — простое число, то Z _n^*, +_п , 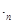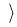является полем. Функция = | Z _n^* | называется функцией Эйлера. Если р — простое число, то 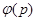= р — 1, и вообще, > (n).

Можно показать, что

где 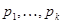— все простые делители n.

Имеет место следующая теорема.

Теорема 6.7. (Эйлера) Если п > 1, то

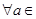Z _n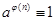^* (mod n).

Отсюда непосредственно выводима

Теорема 6.8. (малая теорема Ферма) Если р > 1 — простое число, то

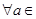Z _p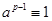^* (mod p).

Имеет место следующее утверждение.

Теорема 6.9. Если числа попарно взаимно простые, число 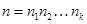—их произведение, х и а — целые числа, то

х = a (mod n) 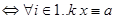(mod n).

Последнее утверждение является следствием теоремы, которая известна как «китайская теорема об остатках».

Шифрование с открытым ключом

Шифрование с открытым ключом производится следующим образом.

1. Получателем сообщений производится генерация открытого ключа (пара чи­сел п и е) и закрытого ключа (число d). Для этого:

- выбираются два простых числа р и q;

- определяется первая часть открытого ключа п == pq;

- определяется вторая часть открытого ключа — выбирается небольшое не­четное число е, взаимно простое с числом (р – 1)(q - 1) (заметим, что (р - 1)(q - 1) = pq (1 - 1/ р)(1 - 1 /q) = );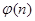

- определяется закрытый ключ: d = е^-1 mod ((р – 1)(q - 1)).

После чего открытый ключ (числа n и е) сообщается всем отправителям со­общений.

2. Отправитель шифрует сообщение (разбивая его, если нужно, на слова S_i, дли­ной менее log₂ п разрядов):

C_i =(S_i) ^e mod n

и отправляет получателю.

3. Получатель расшифровывает сообщение с помощью закрытого ключа d:

Р _i = (С _i) ^d mod n.

Теорема 6.10. Шифрование с открытым ключом корректно, то есть в предыдущих обозначениях P_i = S_i.

Доказательство. Легко видеть, что P_i =(S_i) ^ed mod n. Покажем, что 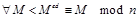. Действительно, числа d и е взаимно обратны по модулю (р – 1)(q - 1), то есть

ed == 1 + k (p - 1)(q - 1)

при некотором k. Если М = 0 (mod р), то по малой теореме Ферма имеем:

.

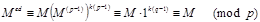Если М 0 (mod р), то сравнение М ^ed =М (mod р), очевидно, выполняется. Таким образом,

.

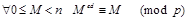Совершенно аналогично имеем

,

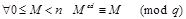и по следствию к китайской теореме об остатках

.

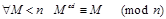Поскольку S_i < п и P_i < п, заключаем, что.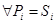

Пример 6.12. Генерация ключей:

1. р =3, q:=11;

2. n = рq =3 11=33;

3. (р – 1)(q - 1) = 2 10 = 20, е = 7;

4. d =7^-1 mod 20=3, (7 3 mod 20 = 1).

Пусть S _l = 3, S ₂ = 1, S ₃ = 2 (S _l, S ₂, S ₃ < п = 33). Тогда код определяется сле­дующим образом.

1. C ₁ = З⁷ mod 33 = 2187 mod 33 = 9;

2. C ₂ = I⁷ mod 33 = 1 mod 33 = 1;

3. C ₃ = 2⁷ mod 33 = 128 mod 33 = 29.

При расшифровке имеем:

1. P ₁ = 9³ mod 33 = 729 mod 33 = 3;

2. P ₂ = 1³ mod 33 = 1 mod 33 = 1;

3. P ₃ = 29³ mod 33 = 24389 mod 33 = 2.

Шифры с открытым ключом сравнительно просты в реализации, очень практичны (по­скольку нет необходимости пересылать по каналам связи закрытый ключ и можно без­опасно хранить его в одном месте) и в то же время обладают высочайшей криптостойкостыо. Кажется, что дешифровать сообщение несложно: достаточно разложить открыто опубликованное число п на множители, восстановив числа р и q, и далее можно легко вычислить секретный ключ d. Однако дело заключается в следующем. В настоящее время известны эффективные алгоритмы определения простоты чисел, которые позволяют за несколько минут подобрать пару очень больших простых чисел (по 100 и больше цифр в десятичной записи). В то же время неизвестны эффективные алгоритмы разложения очень больших чисел на множители. Разложение на множители числа в 200 и больше цифр потребовало бы сотен лет работы самого лучшего суперкомпьютера. При практическом применении шифров с открытым ключом используют действительно большие простые числа (не менее 100 цифр в десятичной записи, а обычно значительно больше). В ре­зультате вскрыть этот шифр оказывается невозможным, если не существует эффективных алгоритмов разложения на множители (что очень вероятно, хотя и не доказано строго).

Поиск по сайту: