Схема кодирования Фано

Кодирование

Вопросы кодирования издавна играли заметную роль в математике. Например:

1. Десятичная позиционная система счисления — это способ кодирования нату­ральных чисел. Римские цифры — другой способ кодирования натуральных чисел, причем гораздо более наглядный и естественный: палец — I, пятерня — V, две пятерни — X. Однако при этом способе кодирования труднее выполнять арифметические операции над большими числами, поэтому он был вытеснен позиционной десятичной системой.

2. Декартовы координаты — способ кодирования геометрических объектов чи­слами.

3. Составление текста программы часто и совершенно справедливо тоже называют кодиро­ванием.

Ранее вопросы кодирования играли вспомогательную роль и не рассматривались как отдельный предмет математического аппарата, но с появлением средств связи и особенно компьютеров ситуация радикально изменилась. Кодирование буквально пронизывает инфор­мационные технологии и является одним из центральных вопросов при решении самых разных задач программирования и информационных процессов:

- представление данных произвольной природы (например, чисел, текста, гра­фики) в памяти компьютера;

- защита информации от несанкционированного доступа;

- обеспечение помехоустойчивости при передаче данных по каналам связи;

- сжатие информации в базах данных.

Не ограничивая общности, задачу кодирования можно сформулировать следу­ющим образом. Пусть заданы алфавиты А = { a ₁,..., a_n }, В = { b ₁,…, b_m } и функция F: S В^*, где S — некоторое множество слов в алфавите A, S А^*. Тогда функция F называется кодированием, элементы множества S — сообщения­ми, а элементы множества В — кодами (соответствующих сообщений). Обратная функция F^-1 (если она существует!) называется декодированием.

Если | В | = m, то F называется т-ичным кодированием. Наиболее распространен­ный случай В = {0,1} — двоичное кодирование. Именно этот случай рассматри­вается в последующих разделах; слово «двоичное» опускается.

Типичная задача теории кодирования формулируется следующим образом: при заданных алфавитах А, В и множестве сообщений S найти такое кодирование F, которое обладает определенными свойствами (то есть удовлетворяет заданным ограничениям) и оптимально в некотором смысле. Критерий оптимальности, как правило, связан с минимизацией длин кодов. Свойства, которые требуются от кодирования, бывают самой разнообразной природы:

- существование декодирования — это очень естественное свойство, однако даже оно требуется не всегда. Например, трансляция на ЭВМ программы на языке высокого уровня в машинные команды — это кодирование, для которого не требуется однозначного декодирования;

- помехоустойчивость, или исправление ошибок: функция декодирования F ^{- 1} обладает таким свойством, что 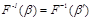, если в определенном смысле близко к (см. раздел 6.3);

- заданная сложность (или простота) кодирования и декодирования. Например, в криптографии изучаются такие способы кодирования, при которых имеется просто вычисляемая функция F, но определение функции F^-1 требует очень сложных вычислений (см. раздел 6.5.).

Большое значение для задач кодирования имеет природа множества сообщений S. При одних и тех же алфавитах А, В и требуемых свойствах кодирования f оптимальные решения могут кардинально отличаться для разных S. Для описа­ния множества S (как правило, очень большого или бесконечного) применяются различные методы:

-теоретико-множественное описание, например

-вероятностное описание, например S = А*, и заданы вероятности р, появление букв в сообщении, ;

-логико-комбинаторное описание, например, S задано порождающей формальной грамматикой.

6.1. Алфавитное кодирование

Кодирование F может сопоставлять код всему сообщению из множества S как единому целому или же строить код сообщения из кодов его частей. Элемен­тарной частью сообщения является одна буква алфавита А. Этот простейший случай рассматривается ниже.

Пусть задано конечное множество А = { a₁,..., a_n }, которое называется алфави­том. Элементы алфавита называются буквами. Последовательность букв называ­ется словом (в данном алфавите). Множество слов в алфавите А обозначается А^*. Если слово , то количество букв в слове называется длиной сло­ва:

Пустое слово обозначается

Если то называется началом, или префиксом, слова , а 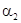— оконча­нием, или постфиксом слова . Если при этом (соответственно, ), то (соответственно, ) называется собственным началом (соотвественно, соб­ственным окончанием) слова .

Алфавитное (или побуквенное) кодирование задается схемой (или таблицей ко­дов) :

Множество кодов букв V: ={ } называется множеством элементарных кодов. Алфавитное кодирование пригодно для любого множества сообщений S:

Пример 6.1. Рассмотрим алфавиты A ={0,1,2,3,4,5,6,7,8,9}, В: ={0,1} и схему

.

Эта схема однозначна, но кодирование не является взаимно однозначным:

а значит, невозможно декодирование. С другой стороны, схема

известная под названием «двоично-десятичное кодирование», допускает одно­значное декодирование.

Рассмотрим схему алфавитного кодирования и различные слова, составленные из элементарных кодов. Схема называется разделимой, если

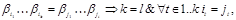
то есть любое слово, составленное из элементарных кодов, единственным обра­зом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование.

Если таблица кодов содержит одинаковые элементарные коды, то есть, если

где , то схема заведомо не является разделимой. Такие схемы далее не рассматриваются, то есть

Схема называется префиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы:

Теорема 6.1. Префиксная схема является разделимой.

Доказательство. От противного. Пусть кодирование со схемой не является разделимым. Тогда существует такое слово , что

.

Поскольку , значит, , но это противоречит тому, что схема префиксная. Свойство быть префиксной является достаточным, но не является необходимым для раз­делимости схемы.

Пример 6.2. Разделимая, но не префиксная схема: А = { а,b }, В = {0, 1}, S = { а 0, b 01}.

Чтобы схема алфавитного кодирования была разделимая, необходимо, чтобы длины элементарных кодов удовлетворяли определенному соотношению, извест­ному как неравенство Макмиллана.

Теорема 6.2. Если схема разделима, то

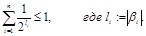
Доказательство. Обозначим . Рассмотрим п- ю степень левой части неравенства

Раскрывая скобки, имеем сумму

,

где — различные наборы номеров элементарных кодов. Обозначим через количество входящих в эту сумму слагаемых вида 1/2 ^t, где . Для некоторых t может быть, что v(n, t) = 0. Приводя подобные, имеем сумму

.

Каждому слагаемому вида можно однозначно сопоставить код (слово в алфавите В) вида . Это слово состоит из п элементарных кодов и имеет длину t.

Таким образом, v(n,t) — это число некоторых слов вида , таких что = t. В силу разделимости схемы v(n, t) в противном случае заведомо существовали бы два одинаковых слова = 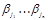, допус­кающих различное разложение. Имеем

Следовательно, , и значит, , откуда

что и требовалось доказать.

Неравенство Макмиллана является не только необходимым, но и в некотором смысле достаточным условием разделимости схемы алфавитного кодирования.

Теорема 6.3. Если числа удовлетворяют неравенству

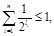
то существует разделимая схема алфавитного кодирования

, где .

Доказательство. Без ограничений общности можно считать, что . Разобьем мно­жество { } на классы эквивалентности по равенству , т п. Пусть

Тогда неравенство Макмиллана можно записать так:

Из этого неравенства следуют m неравенств для частичных сумм:

,

,

Рассмотрим слова длины в алфавите В. Поскольку , из этих слов можно выбрать различных слов длины . Исключим из дальней­шего рассмотрения все слова из В^*, начинающиеся со слов . Далее рассмотрим множество слов в алфавите В длиной и не начинающихся со слов . Таких слов будет . Но , значит, можно выбрать различных слов. Обозначим их . Исключим слова, начинающиеся с из дальнейшего рассмотрения. И так далее, используя неравенства для частичных сумм, мы будем на i -м шаге выби­рать 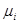слов длины , , причем эти слова не будут начинаться с тех слов, которые были выбраны раньше. В то же время длины этих слов все время растут (так как ), поэтому они не могут быть префиксами тех слов, которые выбраны раньше. Итак, в конце имеем набор из п слов , коды не являются префиксами друг друга, а значит, схема будет префиксной и, по теореме предыдущего подраздела, разделимой.

Пример 6.3. Азбука Морзе — это схема алфавитного кодирования:

А 01, В 1000, C 1010, D 100, Е 0, F 0010, G 110, H 0000, I 00, J 0111, K 101, L 0100, М 11, N 10, O 111, Р 0110, Q 1101, R 010, S 000, T 1, U 001, V 0001, W 011, X 1001, Y 1011, Z 1100 ,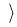

где по историческим и техническим причинам 0 называется точкой и обознача­ется знаком «•», а 1 называется тире и обозначается знаком «—». Имеем:

1/4 + 1/16 + 1/16 + 1/8 + 1/2 + 1/16 + 1/8 + 1/16 + 1/4 + 1/16 +

+ 1/8 + 1/16 + 1/4 + 1/4 + 1/8 + 1/16 + 1/16 + 1/8 + 1/8 +

+ 1/2 + 1/8 + 1/16 + 1/8 + 1/16 + 1/16 + 1/16 =

= 2/2 + 4/4 + 7/8 + 12/16 = 3 + 5/8 > 1.

Таким образом, неравенство Макмиллана для азбуки Морзе не выполнено, и эта схема не является разделимой. На самом деле в азбуке Морзе имеются дополни­тельные элементы — паузы между буквами (и словами), которые позволяют де­кодировать сообщения. Эти дополнительные элементы определены неформаль­но, поэтому прием и передача сообщений с помощью азбуки Морзе, особенно с высокой скоростью, является некоторым искусством, а не простой технической процедурой.

6.2. Кодирование с минимальной избыточностью

Для практики важно, чтобы коды сообщений имели по возможности наимень­шую длину. Алфавитное кодирование пригодно для любых сообщений, то есть S = А^*. Если больше про множество S ничего не известно, то точно сформули­ровать задачу оптимизации затруднительно. Однако на практике часто доступна дополнительная информация. Например, для текстов на естественных языках известно распределение вероятности появления букв в сообщении. Использова­ние такой информации позволяет строго поставить и решить задачу построения оптимального алфавитного кодирования.

Если задана разделимая схема алфавитного кодирования , то лю­бая схема , где является перестановкой , также будет разделимой. Если длины элементарных кодов равны, то перестанов­ка элементарных кодов в схеме не влияет на длину кода сообщения. Но если дли­ны элементарных кодов различны, то длина кода сообщения зависит от состава букв в сообщении и от того, какие элементарные коды каким буквам назначены.

Если заданы конкретное сообщение и конкретная схема кодирования, то нетруд­но подобрать такую перестановку элементарных кодов, при которой длина кода сообщения будет минимальна.

Пусть — количества вхождений букв в сообщение S, а — длины элементарных кодов , соответственно. Тогда, если , и , то . Действительно, пусть и , где Тогда

Отсюда вытекает алгоритм назначения элементарных кодов, при котором длина кода конкретного сообщения S будет минимальна: нужно отсортировать буквы в порядке убывания количества вхождений, элементарные коды отсортировать в порядке возрастания длины и назначить коды буквам в этом порядке. Следует заметить, что этот простой метод решает задачу минимизации длины кода только для фиксированного сообщения S и фиксированной схемы .

Пусть заданы алфавит А == и вероятности появления букв в сооб­щении ( — вероятность появления буквы ). Не ограничивая общности, можно считать, что и (то есть можно сразу исключить буквы, которые не могут появиться в сообщении, и упорядочить буквы по убыванию вероятности их появления).

Для каждой (разделимой) схемы алфавитного кодирования ма­тематическое ожидание коэффициента увеличения длины сообщения при коди­ровании (обозначается ) определяется следующим образом:

, где

и называется средней ценой (или длиной) кодирования при распределении ве­роятностей Р.

Пример 6.4. Для разделимой схемы А = {а, b }, В = {0,1}, при распреде­лении вероятностей цена кодирования составляет 0.5 1 + 0.5 2 = 1.5, а при распределении вероятностей она равна 0.9 1 + 0.1 2 = 1.1.

Обозначим

Очевидно, что всегда существует разделимая схема такая что . Такая схема называется схемой равномерного кодирования. Следова­тельно, 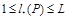1 и достаточно учитывать только такие схемы, для которых , где — целое и . Таким образом, имеется лишь конечное число схем , для которых . Следовательно, существует схема , на которой инфимум достигается: .

Алфавитное (разделимое) кодирование , для которого называ­ется кодированием с минимальной избыточностью, или оптимальным кодирова­нием, для распределения вероятностей Р.

Схема кодирования Фано

Данный алгоритм строит разделимую префиксную схему алфавитного кодирования, близкого к оптимальному. Он основан на теореме Шеннона о том, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число символов на букву будет сколь угодно близко к энтропии Н (меры неопределенности, определяющей количество информации в сообщении) источника сообщений, но не меньше этой величины:

,

где z _i – символ алфавита, а p(z _i ) – вероятность его появления в сообщении.

В алгоритме полагается, что известна длина алфавита n и построен массив убывающей последовательности вероятностей p(z _i ):

.

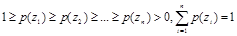Сначала все символы разделяются на две группы так, чтобы суммарная вероятность одной и другой групп были очень близкими. В первой группе первый символ кода устанавливаем равным 0, во второй – 1. Каждая из полученных подгрупп в свою очередь разбивается на две подгруппы с одинаковыми (или почти одинаковыми) вероятностями. Верхней подгруппе приписываем справа 0, а нижней –1 и т.д.

Процесс повторяем пока в каждой подгруппе не останется по одной букве.

Для повторяющейся процедуры отыскания индекса, при котором суммарные вероятности подгрупп близки (назовем его медианой), структура алгоритма может иметь следующий вид.

Входная информация: массив вероятностей , начальный (i₀) и конечный (i_f) индекс в анализируемой группе. Отыскивается индекс m элемента, такого что он является решением задачи

.

Назовем процедуру В ней - сумма элементов верхней части группы, - нижней.

Шаг 1. Полагаем

Шаг 2. Находим в цикле сумму .

Шаг 3. Полагаем .

Шаг 4. Полгаем .

Шаг 5. Проверка. Если идти к шагу 4, иначе останов. Найденное m является медианой.

Вторая повторяющаяся процедура – построение k+1 –го символа в коде (k=1,2,…,L). На входе в процедуру имеем индексы начала и конца обрабатываемой группы, k – длина уже построенных кодов в обрабатываемой части массива кодов С, который является массивом размером n ´ L и CijÎ{0,1}. Выходом является полностью построенный массив С.

Предлагаемый алгоритм носит рекурсивный характер, и обращение к нему обозначим Тогда его структура имеет следующий вид.

Шаг 1. Проверка на окончание. Если i_f = i₀, то работа алгоритма окончена, и двумерный массив С сформирован. Идти к шагу 6. Иначе перейти к шагу 2.

Шаг 2. Подготовка очередного разряда в коде. Полагаем k=k+1. Находим медиану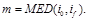

Шаг 3. Формируем матрицу С.

0, если i Î[ i₀,m ],

1, если i Î[ m+1,i_f ].

Шаг 4. Обработка верхней части группы

Шаг 5. Обработка нижней части группы

Шаг 6. Останов.

Тогда основной алгоритм состоит из ввода упорядоченного массива , вызова процедуры и вывода матрицы С.

Обоснование. При каждом удлинении кодов в одной части коды удлиняются нулями, а в дру­гой — единицами. Таким образом, коды одной части не могут быть префиксами другой. Удлинение кода заканчивается тогда и только тогда, когда длина части равна 1, то есть остается единственный код. Таким образом, схема по построению префиксная, а потому разделимая.

Пример 6.5. Коды, построенные алгоритмом Фано для заданного распределения вероятностей (n =7).

PI	С [ i ]	li
0.20		2
0.20
0.19
0.12
0.11
0.09
0.09
=2.80   2.80

Наибольший эффект сжатия сообщения получается в случае, когда вероятности букв представляют собой целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии.

Поиск по сайту: