Схема кодирования Хаффмена

Рассмотренная ранее схема Фано построения кода не всегда приводит к однозначному его построению. Ведь при разбиении на подгруппы можно сделать большой по вероятности как верхнюю, так и нижнюю подгруппы. Тем самым построенный код может оказаться не самым лучшим.

От указанного недостатка свободна схема Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Для двоичного кода схема сводится к следующему. Выстраиваем символы алфавита в убывающей последовательности по вероятности появления символов в сообщении. Два последних объединяются в один вспомогательный символ, которому приписывается суммарная вероятность. И снова в новой последовательности производится построение убывающей последовательности. Два последних символа объединяются опять. Процесс продолжается до тех пор, пока не получим единственный символ с вероятностью, равной единице.

Для составления кодовой комбинации для наглядности строится кодовое дерево. Из точки, соответствующей вероятности 1, исходят две дуги, причем дуге с большей вероятностью присваивается 1, а меньшей 0. Такие последовательные ветвления продолжаем до тех пор, пока не дойдем до вероятностей каждого символа (рис. 6.1.).

Двигаясь теперь по дереву к каждой из их тупиковых вершин, соответствующих символам, можем записать для каждого символа код.

Пример 6.6. Построение оптимального кода Хаффмена для данных, которые уже использовались для построения кода Фано. Показано на изображенной ниже схеме, где стрелками показаны переходы «объединенных» символов.

Иллюстрация кодирования продемонстрирована на рис. 6.1., где изображено кодовое дерево.

Цена кодирования составляет

0.20 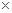2+0.20 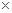2+0.19 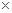34-0.12 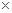3+0.11 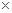3+0.09 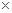4+0.09 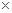4=2.78, что несколько лучше, чем в кодировании, полученном алгоритмом Фано.

Рис 6.1. Кодовое дерево, построенное для схемы кодирования Хаффмена

6.3. Помехоустойчивое кодирование.

Надежность электронных устройств по мере их совершенствования все время возрастает, но, тем не менее, в их работе возможны ошибки, как систематиче­ские, так и случайные. Сигнал в канале связи может быть искажен помехой, по­верхность магнитного носителя может быть повреждена, в разъеме может быть потерян контакт. Ошибки аппаратуры ведут к искажению или потере передавае­мых или хранимых данных. При определенных условиях, некоторые из которых рассматриваются в этом разделе, можно применять методы кодирования, позво­ляющие правильно декодировать исходное сообщение, несмотря на ошибки в данных кода. В качестве исследуемой модели достаточно рассмотреть канал свя­зи с помехами, потому что к этому случаю легко сводятся остальные. Например, запись на диск можно рассматривать как передачу данных в канал, а чтение с диска — как прием данных из канала.

Кодирование с исправлением ошибок

Пусть имеется канал связи С, содержащий источник помех:

,

где S — множество переданных, а S' — соответствующее множество принятых по каналу сообщений. Кодирование F, обладающее таким свойством, что

называется помехоустойчивым или самокорректирующимся, или кодированием с исправлением ошибок.

Без ограничения общности можно считать, что А = В = {0,1}, и что содержа­тельное кодирование выполняется на устройстве, свободном от помех.

Поиск по сайту: