Классификация ошибок. Ошибки в канале могут быть следующих типов:

Ошибки в канале могут быть следующих типов:

а) 0 1, 1 0 — ошибка типа замещения разряда;

б) 0 , 1 — ошибка типа выпадения разряда;

в) 1, 0 — ошибка типа вставки разряда.

Канал характеризуется верхними оценками количества ошибок каждого типа, которые возможны при передаче через канал сообщения определенной длины. Общая характеристика ошибок канала (то есть их количество и типы) обознача­ется S.

Пример 6.7. Допустим, что имеется канал с характеристикой = (1,0,0), то есть в канале воз­можна одна ошибка типа замещения разряда при передаче сообщения длины n. Рассмотрим следующее кодирование: F(a): = ааа (то есть каждый разряд в со­общении утраивается) и декодирование F^-1 (abc): = а+b+с > 1 (то есть разряд восстанавливается методом «голосования»). Это кодирование кажется помехо­устойчивым для данного канала, однако на самом деле это не так. Дело в том, что при передаче сообщения длины 3 n возможно не более 3 ошибок типа заме­щения разряда, но места этих ошибок совершенно не обязательно распределены равномерно по всему сообщению. Ошибки замещения могут произойти в сосед­них разрядах, и метод голосования восстановит разряд неверно.

Возможность исправления всех ошибок

Пусть 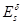— множество слов, которые могут быть получены из слова s в ре­зультате всех возможных комбинаций допустимых в канале ошибок , то есть . Если , то та конкретная последовательность оши­бок, которая позволяет получить из слова s слово s', обозначается {s, s'}. Если тип возможных ошибок в канале подразумевается, то индекс не указывается.

Теорема 6.5. Чтобы существовало помехоустойчивое кодирование с исправлением всех ошибок, необходимо и достаточно, чтобы Ø, то есть необходимо и достаточно, чтобы существовало разбиение множества В* на множества 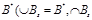= Ø), такое что .

Доказательство. Если кодирование помехоустойчивое, то очевидно, что Ø. Обратно: по разбиению ( строится функция F^-1: ).

Пример 6.8. Рассмотрим канал, в котором в любом передаваемом разряде происходит ошибка типа замещения с вероятностью р (0 < р < 1/2), причем замещения различных разрядов статистически независимы. Такой канал называется двоичным симме­тричным. В этом случае любое слово может быть преобразовано в любое другое слово замещениями разрядов. Таким образом, 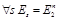, и исправить все ошибки в двоичном симметричном канале невозможно.

Кодовое расстояние

Неотрицательная функция d(x, у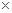): М М R₊ называется расстоянием (или метрикой) на множестве М, если выполнены следующие условия (аксиомы ме­трики):

1. d(x,y) = 0 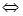х=у,

2. d(x,y) =d(y,x),

3. d(x, у) d(x,z) + d(y, z).

Пусть

Эта функция называется расстоянием Хемминга.

Следует отметить, что мы рассматриваем симметричные ошибки, то есть если в канале допустима ошибка 0 1, то допустима и ошибка 1 0.

Введенная функция является расстоянием. Действительно:

1. 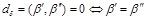, поскольку ошибки симметричны, и из последова­тельности можно получить последовательность , применяя обратные ошибки в обратном порядке.

2. по той же причине.

3. , поскольку 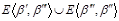является некоторой последовательностью, преобразующей в , а является кратчайшей из таких последовательностей.

Пусть ^— схема некоторого алфавитного кодирования, a d — некоторая метрика на В*. Тогда минимальное расстояние между элементарными кодами

называется кодовым расстоянием схемы .

Теорема 6.6. Алфавитное кодирование со схемой и с кодовым рас­стоянием

является кодированием с исправлением р ошибок типа тогда и только тогда, когда .

Доказательство. E(x) — это шар радиуса р с центром в х для канала, который допускает не более р ошибок типа . Таким образом,

Ø

по теореме 6.5.

Пример 6.9. Расстояние Хэмминга в

Код Хэмминга для исправления одного замещения

Рассмотрим построение кода Хэмминга, который позволяет исправлять одиноч­ные ошибки типа замещения. Очевидно, что для исправления ошибки вместе с основным сообщением нужно передавать какую-то дополнительную информацию.

Пусть сообщение 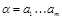кодируется словом , п > т. Обозна­чим k:= п — т. Пусть канал допускает не более одной ошибки типа замещения в слове длины n.

Отметим, что рассматриваемый случай простейший, но одновременно практически очень важный. Та­ким свойством, как правило, обладают внутренние шины передачи данных в современных компьютерах.

При заданном п количество дополнительных разрядов k подбирается таким обра­зом, чтобы . Имеем:

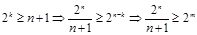
Пример 6.10. Для сообщения длиной т = 32 потребуется k == 6 дополнительных разрядов, поскольку 64 = 2⁶ > 32 + 6 + 1 == 39.

Определим последовательности натуральных чисел в соответствии с их предста­влениями в двоичной системе счисления следующим образом:

- V ₁ = 1,3,5,7,9,11,... — все числа, у которых разряд №1 равен 1;

- V ₂ = 2,3,6,7,10,... — все числа, у которых разряд №2 равен 1;

- V ₃ = 4,5,6,7,12,... — все числа, у которых разряд №3 равен 1,

и т. д. По определению, последовательность V_k начинается с числа 2 ^k-1.

Рассмотрим в слове k разрядов с номерами 2⁰ = 1, 2¹ = 2, 2² = 4,... 2 ^{k -l}. Эти разряды назовем контрольными. Остальные разряды, а их ровно т, назовем информационными. Поместим в информационные разряды все разряды слова как они есть. Контрольные разряды определим следующим обра­зом:

- b ₁ = b ₃ b ₅ b ₇ ..., — то есть все разряды с номерами из V ₁, кроме первого;

- b ₂ = b ₃ b ₆ b ₇ ..., — то есть все разряды с номерами из V ₂, кроме первого;

- b ₄ = b ₅ b ₆ b ₇ ..., —то есть все разряды с номерами из V ₃, кроме первого;

и вообще,

.

Пусть после прохождения через канал получен код ,

то есть = C(b ₁ ... b_n), причем

Здесь I — номер разряда, в котором, возможно, произошла ошибка замещения. Пусть это число имеет следующее двоичное представление: I = i_l... i ₁.

Определим число J = j_l... j ₁ следующим образом:

- j ₁ = c ₁ c ₃ c ₅ c ₇ ..., — то есть все разряды с номерами из V ₁;

- j ₂ = c ₂ c ₃ c ₆ c ₇ ..., — то есть все разряды с номерами из V ₂;

- j ₃= c ₄ c ₅ c ₆ b ₇ ..., — то есть все разряды с номерами из V ₃;

и вообще,

Теорема 6.7. I =J.

Доказательство. Эти числа равны, потому что поразрядно равны их двоичные представления. Действительно, пусть i ₁= 0. Тогда I , и значит,

=

по определению разряда . Пусть теперь . Тогда I , и значит,

=

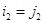так как если в сумме по модулю два изменить ровно один разряд, то изменится и значение всей суммы. Итак, . Аналогично (используя последовательности и т. д.) имеем и т. д. Таким образом, I == J.

Отсюда вытекает метод декодирования с исправлением ошибки: нужно вычи­слить число J. Если J = 0, то ошибки нет, иначе . После этого из ис­правленного сообщения извлекаются информационные разряды, которые уже не содержат ошибок.

6.4. Сжатие данных

Материал раздела 6.2 показывает, что при кодировании наблюдается некоторый баланс между временем и памятью. Затрачивая дополнительные усилия при ко­дировании и декодировании, можно сэкономить память, и, наоборот, пренебрегая оптимальным использованием памяти, можно существенно выиграть во времени кодирования и декодирования. Конечно, этот баланс имеет место только в опре­деленных пределах, и нельзя сократить расход памяти до нуля или построить мгновенно работающие алгоритмы кодирования. Для алфавитного кодирования пределы возможного установлены в разделе 6.2. Для достижения дальнейшего прогресса нужно рассмотреть неалфавитное кодирование.

Сжатие текстов

Допустим, что имеется некоторое сообщение, которое закодировано каким-то об­щепринятым способом (для текстов это, например, код ASCII) и хранится в па­мяти компьютера. Заметим, что равномерное кодирование (в частности, ASCII) не является оптимальным для текстов. Действительно, в текстах обычно исполь­зуется существенно меньше, чем 256 символов (в зависимости от языка — при­мерно 60-80 с учетом знаков препинания, цифр, строчных и прописных букв). Кроме того, вероятности появления букв различны и для каждого естественного языка известны (с некоторой точностью) частоты появления букв в тексте. Та­ким образом, можно задаться некоторым набором букв и частотами их появления в тексте и с помощью алгоритма Хаффмена построить оптимальное алфавитное кодирование текстов (для заданного алфавита и языка). Простые расчеты по­казывают, что такое кодирование для распространенных естественных языков будет иметь цену кодирования несколько меньше 6, то есть даст выигрыш по сравнению с кодом ASCII на 25% или несколько больше.

Методы кодирования, которые позволяют построить (без потери информации!) коды со­общений, имеющие меньшую длину по сравнению с исходным сообщением, называются методами сжатия (или упаковки) данных. Качество сжатия определяется коэффициентом сжатия, который обычно измеряется в процентах и показывает, на сколько процентов кодированное сообщение короче исходного.

Известно, что практические программы сжатия (arj, zip и другие) имеют гораздо лучшие показатели: при сжатии текстовых файлов коэффициент сжатия достига­ет 70% и более. Это означает, что в таких программах используется не алфавитное кодирование.

Предварительное построение словаря

Рассмотрим следующий способ кодирования.

1. Исходное сообщение по некоторому алгоритму разбивается на последователь­ности символов, называемые словами (слово может иметь одно или несколько вхождений в исходный текст сообщения).

2. Полученное множество слов считается буквами нового алфавита. Для этого алфавита строится разделимая схема алфавитного кодирования (равномер­ного кодирования или оптимального кодирования, если для каждого слова подсчитать число вхождений в текст). Полученная схема обычно называется словарем, так как она сопоставляет слову код.

3. Далее код сообщения строится как пара — код словаря и последовательность кодов слов из данного словаря.

4. При декодировании исходное сообщение восстанавливается путем замены ко­дов слов на слова из словаря.

Пример 6.11. Допустим, что требуется кодировать тексты на русском языке. В качестве алго­ритма деления на слова примем естественные правила языка: слова отделяются друг от друга пробелами или знаками препинания. Можно принять допущение, что в каждом конкретном тексте имеется не более 2¹⁶ различных слов (обычно гораздо меньше). Таким образом, каждому слову можно сопоставить номер — це­лое число из двух байтов (равномерное кодирование). Поскольку в среднем слова русского языка состоят более чем из двух букв, такое кодирование дает суще­ственное сжатие текста (около 75% для обычных текстов на русском языке). Если текст достаточно велик (сотни тысяч или миллионы букв), то дополнительные затраты на хранение словаря оказываются сравнительно небольшими.

Данный метод попутно позволяет решить задачу полнотекстового поиска, то есть опре­делить, содержится ли заданное слово (или слова) в данном тексте, причем для этого не нужно просматривать весь текст (достаточно просмотреть только словарь).

Указанный метод можно усовершенствовать следующим образом. На шаге 2 сле­дует применить алгоритм Хаффмена для построения оптимального кода, а на ша­ге 1 — решить экстремальную задачу разбиения текста на слова таким образом, чтобы среди всех возможных разбиений выбрать то, которое дает наименьшую цену кодирования на шаге 2. Такое кодирование будет «абсолютно» оптималь­ным. К сожалению, указанная экстремальная задача очень трудоемка, поэтому на практике не используется — время на предварительную обработку большого текста оказывается чрезмерно велико.

На практике используется следующая идея, которая известна также как ада­птивное сжатие. За один проход по тексту одновременно динамически строится словарь и кодируется текст. При этом словарь не хранится — за счет того, что при декодировании используется тот же самый алгоритм построения словаря, словарь динамически восстанавливается.

6.5. Шифрование и криптография.

Защита компьютерных данных от несанкционированного доступа, искажения и уничтожения в настоящее время является серьезной социальной проблемой. Применяются различные подходы к решению этой проблемы. Прежде всего, надо поставить между злоумышленником и данными в компьютере логический ба­рьер, то есть проверить наличие прав на доступ к данным и блокировать до­ступ при их отсутствии. Для этого применяются различные системы паролей, регистрация и идентификация пользователей, разграничения прав доступа и т. п. Практика показывает, что борьба между «хакерами» и модуля­ми защиты операционных систем идет с переменным успехом. Дополнительные меры в этой борьбе - хранить данные таким образом, чтобы они могли «сами за себя постоять». Другими словами, так закодировать данные, чтобы даже получив их, злоумыш­ленник не смог бы нанести ущерба.

Шифрование — это кодирование данных с целью защиты от несанкционированного доступа. Процесс кодирования сообщения называется шифрованием (или зашифровкой), а процесс декодирования — расшифровыванием (или расшифровкой). Само коди­рованное сообщение называется шифрованным (или просто шифровкой), а при­меняемый метод называется шифром.

Основное требование к шифру состоит в том, чтобы расшифровка (и, может быть, зашифровка) была возможна только при наличии санкции, то есть некото­рой дополнительной информации (или устройства), которая называется ключом шифра. Процесс декодирования шифровки без ключа называется дешифрованием (или дешифрацией, или просто раскрытием шифра).

Область знаний о шифрах, методах их создания и раскрытия называется кри­птографией (или тайнописью). Свойство шифра противостоять раскрытию называется криптостойкостью (или надежностью) и обычно измеряется сложностью алгоритма дешифрации.

В практической криптографии криптостойкость шифра оценивается из экономических со­ображений. Если раскрытие шифра стоит (в денежном выражении, включая необходимые компьютерные ресурсы, специальные устройства и т. п.) больше, чем сама зашифрованная информация, то шифр считается достаточно надежным.

Криптография известна с глубокой древности и использует самые разнообразные шифры как чисто информационные, так и механические. В настоящее время наибольшее практическое значение имеет защита данных в компьютере, поэтому далее рассматриваются программные шифры для сообщений в алфавите {0,1}.

Шифрование с помощью случайных чисел

Пусть имеется датчик псевдослучайных чисел, работающий по некоторому опре­деленному алгоритму. Часто используют следующий алгоритм:

mod с,

где T_i — предыдущее псевдослучайное число, T_i+1 — следующее псевдослучайное число, а коэффициенты а, b, с постоянны и хорошо известны. Обычно с = 2 ⁿ, где п — разрядность процессора, a mod 4 = 1, a b — нечетное. В этом случае последовательность псевдослучайных чисел имеет период с.

Процесс шифрования определяется следующим образом. Шифруемое сообще­ние представляется в виде последовательности слов 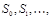каждое длины n, которые складываются по модулю 2 со словами последовательности то есть

Последовательность To,Ti,... называется гаммой шифра. Процесс расшифровывания заключается в том, чтобы еще раз сложить шифро­ванную последовательность с той же гаммой шифра:

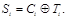
Ключом шифра является начальное значение 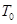, которое является секретным и должно быть известно только отправителю и получателю шифрованного сооб­щения. Шифры, в которых для зашифровки и расшифровки используется один и тот же ключ, называются симметричными.

Если период последовательности псевдослучайных чисел достаточно велик, что­бы гамма шифра была длиннее сообщения, то дешифровать сообщение можно только подбором ключа. При увеличении п экспоненциально увеличивается криптостойкость шифра.

Это очень простой и эффективный метод часто применяют «внутри» программных систем, например, для защиты данных на локальном диске. Для защиты данных, передаваемых по открытым каналам связи, особенно в случае многостороннего обмена сообщениями, этот метод применяют не так часто, поскольку возникают трудности с надежной передачей секретного ключа многим пользователям.

Поиск по сайту: