 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Алгебраическое описание метода
Геометрическое описание метода Хорд
Будем искать корень функции f(x). Выберем две начальные точки C 1(x 1; y 1) и C 2(x 2; y 2) и проведем через них прямую. Она пересечет ось абсцисс в точке (x 3;0). Теперь найдем значение функции с абсциссой x 3. Временно будем считать x 3 корнем на отрезке [ x 1; x 2]. Пусть точка C 3 имеет абсцисcу x 3 и лежит на графике. Теперь вместо точек C 1 и C 2 мы возьмём точку C 3 и точку C 2. Теперь с этими двумя точками проделаем ту же операцию и так далее, т.е. будем получать две точки Cn + 1 и Cn и повторять операцию с ними. Таким образом мы будем получать две точки, отрезок, соединяющий которые, пересекает ось абсцисс в точке, значение абсциссы которой можно приближенно считать корнем. Эти действия нужно повторять до тех пор, пока мы не получим значение корня с нужным нам приближением.
Алгебраическое описание метода
Пусть x 1, x 2 − абсциссы концов хорды, y = kx + b − уравнение прямой, содержащей хорду. Найдем коэффициенты k и b из системы уравнений:
.
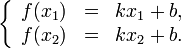Вычтем из первого уравнения второе:
f (x 1) − f (x 2) = k (x 1 − x 2), затем найдем коэффициенты k и b:
, тогда
.
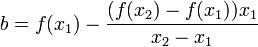Уравнение принимает вид:
Таким образом, теперь можем найти первое приближение к корню, полученное методом хорд:
Теперь возьмем координаты x 2 и x 3 и повторим все проделанные операции, найдя новое приближение к корню. Повторять операцию следует до тех пор, пока xn − xn − 1 не станет меньше или равно заданному значению погрешности.
Вычисления ведутся до тех пор, пока не выполнится неравенство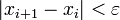 
.
Итерационная формула метода хорд имеет вид 
.
Рассмотрим метод деления отрезка пополам более подробно.
В соответствии с этим методом вначале необходимо приблизительно определить отрезок, на котором функция f(x) меняет знак. Для этого можно использовать графический способ, заключающийся в построении графика функции на экране компьютера и приблизительного визуального определения точек пересечения графика с осью абсцисс.
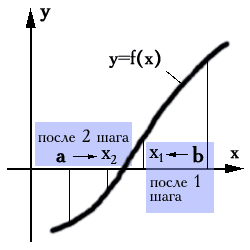При отыскании корня методом половинного деления сначала вычисляются значения функции в точках a и b - соответственно f(a) и f(b), имеющие противоположные знаки. Далее по формуле xср=(a+b)/2 вычисляется координата центра отрезка [a, b] и находится значение функции в этой точке f(xср). Оно сравнивается со значениями функции на концах отрезка. Если функция меняет знак на отрезке [a, xср], то весь отрезок [a, b] усекается до его левой части, то есть xср становится правой границей отрезка (b). Аналогично, если функция меняет знак на отрезке [xср, b], отрезок [a, b] усекается до правой части. Эти операции повторяются до тех пор, пока разница между соседними значениями x не станет меньше или равной выбранной точности e.
Поиск по сайту: