КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ ИНФОРМАЦИИ

Что нужно знать:

· кодирование – это перевод информации с одного языка на другой (запись в другой системе символов, в другом алфавите)

· обычно кодированием называют перевод информации с «человеческого» языка на формальный, например, в двоичный код, а декодированием – обратный переход

· один символ исходного сообщения может заменяться одним символом нового кода или несколькими символами, а может быть и наоборот – несколько символов исходного сообщения заменяются одним символом в новом коде (китайские иероглифы обозначают целые слова и понятия)

· кодирование может быть равномерное и неравномерное;
при равномерном кодировании все символы кодируются кодами равной длины;
при неравномерном кодировании разные символы могут кодироваться кодами разной длины, это затрудняет декодирование

· закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова;

· закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова;

· условие Фано – это достаточное, но не необходимое условие однозначного декодирования.

Пример задания:

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.

1) для буквы Б – 01 2) это невозможно

3) для буквы В – 01 4) для буквы Г – 01

Решение (1 способ, проверка условий Фано):

1) для однозначного декодирования достаточно, чтобы выполнялось условие Фано или обратное условие Фано;

2) проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»);

3) проверяем вариант 1: А–00, Б–01, В–011, Г–101, Д–111.

«прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В);

«обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;

4) проверяем вариант 3: А–00, Б–010, В–01, Г–101, Д–111.

«прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б);

«обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;

5) проверяем вариант 4: А–00, Б–010, В–011, Г–01, Д–111.

«прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит;

6) правильный ответ – 4.

Решение (2 способ, дерево):

1) построим двоичное дерево, в котором от каждого узла отходит две ветки, соответствующие выбору следующей цифры кода – 0 или 1; разместим на этом дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах, составляющих путь от корня до данной буквы (красным цветом выделен код буквы В – 011):

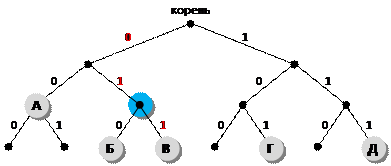
2) здесь однозначность декодирования получается за счёт того, что при движении от корня к любой букве в середине пути не встречается других букв (выполняется условие Фано);

3) теперь проверим варианты ответа: предлагается перенести одну из букв, Б, В или Г, в узел с кодом 01, выделенный синим цветом

4) видим, что при переносе любой из этих букв нарушится условие Фано; например, при переносе буквы Б в синий узел она оказывается на пути от корня до В, и т.д.; это значит, что предлагаемые варианты не позволяют выполнить прямое условие Фано

5) хочется уже выбрать вариант 2 («это невозможно»), но у нас есть еще обратное условие Фано, для которого тоже можно построить аналогичное дерево, в котором движение от корня к букве дает её код с конца (красным цветом выделен код буквы В – 011, записанный с конца):

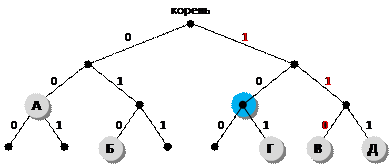
видно, что обратное условие Фано также выполняется, потому что на пути от корня к любой букве нет других букв

6) в заданных вариантах ответа предлагается переместить букву Б, В или Г в синий узел; понятно, что Б или В туда перемещать нельзя – перемещённая буква отказывается на пути от корня к букве Г; а вот букву Г переместить можно, при этом обратное условие Фано сохранится

7) правильный ответ – 4.

Пример задания:

Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится

1) 4B₁₆ 2) 411₁₆ 3)BACD₁₆ 4) 1023₁₆

Решение:

1) из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный

2) последовательность БАВГ кодируется так: 01 00 10 11 = 1001011

3) разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем

1001011 = 0100 1011₂ = 4B₁₆

4) правильный ответ – 1.

Пример задания:

Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110 ). Определите, какое число передавалось по каналу в виде 01010100100111100011?

1) 59143 2) 5971 3) 102153 4) 10273

Решение:

1) сначала разберемся, как закодированы числа в примере; очевидно, что используется код равномерной длины; поскольку 2 знака кодируются 10 двоичными разрядами (битами), на каждую цифру отводится 5 бит, то есть

2 → 00101 и 3 → 00110

2) как следует из условия, четыре первых бита в каждой последовательности – это двоичный код цифры, а пятый бит (бит четности) используется для проверки и рассчитывается как «сумма по модулю два», то есть остаток от деления суммы битов на 2; тогда

2 = 0010₂, бит четности (0 + 0 + 1 + 0) mod 2 = 1

3 = 0011₂, бит четности (0 + 0 + 1 + 1) mod 2 = 0

3) но бит четности нам совсем не нужен, важно другое: пятый бит в каждой пятерке можно отбросить!

4) разобъем заданную последовательность на группы по 5 бит в каждой:

01010, 10010, 01111, 00011.

5) отбросим пятый (последний) бит в каждой группе:

0101, 1001, 0111, 0001.
это и есть двоичные коды передаваемых чисел:

0101₂ = 5, 1001₂ = 9, 0111₂ = 7, 0001₂ = 1.

6) таким образом, были переданы числа 5, 9, 7, 1 или число 5971.

7) Ответ: 2.

Поиск по сайту: