 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Коди з виправленням помилок
Коди з виправленням помилок необхідні для передачі повідомлень каналами зв’язку, оскільки помилки можуть виникати внаслідок впливу завад. Вони потрібні також в зовнішніх запам’ятовуючих пристроях, оскільки якість запису з часом погіршується і надійність читання знижується.
Першими найбільш простими кодами з виправленням помилок є коди з потроєнням. При їх застосуванні передача кожного повідомлення повторюється три рази, а на приймальному кінці для кожного символа здійснюється, так зване, «голосування за більшістю». Зрозуміло, що така система дозволяє виправити будь-які одиночні помилки, зв’язані із заміною символів, але вона є занадто неефективною та дорогою.
4.2.1 Прямокутні коди
В прямокутних кодах з виправленням помилок повідомлення подається у прямокутнику розміром (m-1)´(n-1). До кожного рядка, що складається із m-1 символів, додається перевірка на парність, внаслідок чого рядок стає довжиною m. Аналогічно по одному перевірочному символу додається до кожного стовпчика. При цьому несуттєво, заповнюються чи ні символами повідомлення кінці рядків повністю.
Приклад для m=7, n=8:
| 0 1 1 0 0 1 1 1 1 1 0 0 1 1 0 1 0 1 0 1 0 0 0 1 1 0 0 1 1 0 1 0 1 0 1 | |
| 1 0 1 0 0 1 0 |
Якщо в даному рядку (стовпчику) з’являється одиночна помилка, то порушення парності з’являються одночасно і в n-му стовпчику, і в m-му рядку. Відповідно номери рядка та стовпчика порушення парності дають можливість указати координати помилки в повідомленні.
За рахунок перевірочних символів (m-1)´(n-1) символів повідомлення перетворюються в mn символів коду. Отже, надмірність становить

Звичайною перевіркою легко переконатись, що значення надмірності буде тим меншим, чим ближчий прямокутник до квадрата. Для квадратних кодів розміром m´m є (m-1)2 інформаційних символів і 2´m-1 перевірочних символів вздовж сторін. При цьому надмірність становить
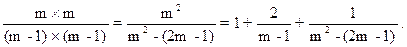
4.2.2 Трикутні коди
Від прямокутних кодів легко перейти до трикутних. Довжини катетів трикутника рівні m. Перевірочні символи, кількість яких теж k, знаходяться на гіпотенузі. Кожний перевірочний символ визначається перевіркою на парність, в яку входять як відповідний рядок, так і відповідний стовпчик.
Помилка повідомлення приводить до порушень парності в двох перевірочних символах. Координати порушень парності дають можливість визначити координати помилки повідомлення.
Приклад для m=5:
1 0 0 1 0
0 1 1 1
1 0 0
0 1
Наприклад, якщо координати помилки повідомлення (2,3), то на порушення парності укажуть перевірочні символи з координатами (2,4) і (3,3). А якщо координати помилки повідомлення (1,4), то на порушення парності укажуть перевірочні символи з координатами (1,5) і (2,4).
Трикутний код дає можливість зменшити надмірність коду. Дійсно, повідомлення в цьому випадку містить m´(m-1)/2 символів, для перевірки додається ще m символів. Отже, надмірність становить

Код Хеммінга
Завадостійкий код, відомий як код Хеммінга, було створено, виходячи із таких передумов:
- повинні виправлятися одиночні помилки, що мають характер «білого шуму»;
- перевірки на парність, кількість яких позначимо m, мають бути незалежними, тобто жодна сума одних перевірок не повинна співпадати з якоюсь іншою перевіркою;
- Для прикладу розглянемо довільний код 100101011, в якому позиції пронумеровані з одиниці зліва направо, а також такі три перевірки цього коду на парність: перша - для позицій 1, 2, 5, 7 (результат 1), друга - для позицій 5, 7, 8, 9 (результат 0) і третя - для позицій 1, 2, 8, 9 (результат 1). Такі перевірки є залежними між собою, оскільки, незалежно від коду, будь-які дві перевірки з цих трьох однозначно визначають результат третьої. Отже, одна з цих перевірок є зайвою.
- синдром довжиною m повинен розрізняти n+1 ситуацію, в тому числі, відсутність помилки, а також положення помилки в одній із будь-яких n позицій коду;
- Ця умова приводить до нерівності 2m ≥ n + 1, з якої можна визначити мінімально допустиме значення m при відомій кількості розрядів двійкового повідомлення k, а саме: n = m + k, звідки 2m ≥ m + k + 1. Наприклад, якщо кількість розрядів повідомлення k = 4, то 2m ≥ m + 5, звідки найменше допустиме m=3. При k = 3 маємо 2m ≥ m + 4 і теж саме m = 3. При k = 5 маємо 2m ≥ m + 6 і m = 4.
- позиції двійкового коду вважають пронумерованими від 1 до n зліва направо і серед них номери позицій для розміщення перевірок на парність вибирають послідовно із ряду 1, 2, 4, 8, 16 і т.д.; в принципі ці номери можуть бути вибрані довільними, але такий ряд вибрано із міркувань зручності обчислень перевірочних позицій; решта позицій є інформаційними;
Наприклад, якщо m=2, то перевірочними будуть 1 і 2 позиції. При m=3 перевірочними позиціями будуть 1, 2 і 4. При m=4 перевірочними позиціями будуть 1, 2, 4 і 8. Чисельне значення синдрому повинно співпадати з номером позиції, в якій виникла помилка, а нульове значення синдрому повинно означати відсутність помилки.
Для забезпечення такої властивості синдрому використовують двійкові подання номерів позицій
| Номер позиції | Двійкове подання | Номер позиції | Двійкове подання | Номер позиції | Двійкове подання |
Першою перевіркою на парність будемо утворювати перше перевірочне значення і наймолодший розряд синдрому. Для цього в першу перевірку слід включити позиції, номери яких мають 1 теж в наймолодших розрядах. Таким чином, в першу перевірку на парність входять позиції 1, 3, 5, 7, 9, 11, 13, 15.
Другою перевіркою на парність будемо утворювати друге перевірочне значення і наступний за наймолодшим розряд синдрому. Для цього в другу перевірку слід включити позиції, номери яких мають 1 теж в наступних за наймолодшими розрядах. Отже, в другу перевірку на парність мають входити позиції 2, 3, 6, 7, 10, 11, 14, 15.
Аналогічно, в третю перевірку на парність мають входити позиції 4, 5, 6, 7, 12, 13, 14, 15, в четверту - позиції 8, 9, 10, 11, 12, 13, 14, 15 і т.д.
Приклад 1. Побудуємо код Хеммінга для 4-розрядного двійкового повідомлення 1011. При цьому n=7, m=3, перевірочні позиції 1, 2, 4.
| Позиції | 1 2 3 4 5 6 7 |
| Повідомлення | _ _ 1 _ 0 1 1 |
| Перша позиція коду (1, 3, 5, 7) | 0 _ 1 _ 0 1 1 |
| Друга позиція коду (2, 3, 6, 7) | 0 1 1 _ 0 1 1 |
| Четверта позиція коду (4, 5, 6, 7) | 0 1 1 0 0 1 1 |
Приклад 2. Код повідомлення з помилкою має вигляд 0100011. Застосуємо перевірки на парність за методикою Хеммінга для виправлення помилки.
| Позиції | 1 2 3 4 5 6 7 |
| Код повідомлення | 0 1 0 0 0 1 1 |
| Синдром | _ _ _ |
| Перша перевірка (1, 3, 5, 7) | _ _ 1 |
| Друга перевірка (2, 3, 6, 7) | _ 1 1 |
| Третя перевірка (4, 5, 6, 7) | 0 1 1 |
Утворений синдром відповідає номеру позиції 3. Тому треба значення третьої позиції коду повідомлення змінити на протилежне. Код повідомлення після виправлення помилки має вигляд 0110011. Відкидаючи перевірочні позиції, отримуємо правильне повідомлення 1011.
Відмітимо, що разом з інформаційними позиціями захищеними виявляються також і перевірочні позиції.
Приклад 3. Код повідомлення з помилкою має вигляд 0111011. Застосуємо перевірки на парність за методикою Хеммінга для виправлення помилки.
| Позиції | 1 2 3 4 5 6 7 |
| Код повідомлення | 0 1 1 1 0 1 1 |
| Синдром | _ _ _ |
| Перша перевірка (1, 3, 5, 7) | _ _ 0 |
| Друга перевірка (2, 3, 6, 7) | _ 0 0 |
| Третя перевірка (4, 5, 6, 7) | 1 0 0 |
Утворений синдром відповідає номеру позиції 4, яка є перевірочною. У виправленні помилки потреби немає. Правильне повідомлення 1011.
Код Грея
Особливості коду Грея розглянемо на прикладі переходу від аналогового подання даних до цифрового.
Розглянемо магнітний носій інформації у вигляді стрічки, на якій у поперечних напрямах розташовано двійкові коди порядкових номерів зон цієї стрічки.
| 0 1 0 |
| 0 1 1 |
| 1 0 0 |
| 1 0 1 |
| 1 1 0 |
Розглянемо порозрядний пристрій читання номерів зон стрічки. Припустимо, що при низькій якості регулювання цього пристрою спроба зчитування відбувається в момент зміни номерів зон. Якщо при цьому на стрічці певний розряд змінюється з 0 на 1 або навпаки, то з пристрою зчитування можна одержати будь-яке значення. Зокрема, при зміні номера з 011 на 100 можна одержати будь-яке з вісьми можливих чисел, і із них шість будуть помилковими.
Тепер представимо собі, що сусідні номери відрізняються між собою лише тільки одним розрядом (наприклад, номери 010 і 011). Тоді за таких же умов результатом зчитування обов’язково буде один із цих номерів, тобто помилки не буде.
Код Грея - це такий метод двійкового кодування, при якому сусідні числові значення відрізняються між собою лише тільки одним розрядом. За рахунок цієї властивості код Грея дозволяє виявляти одиночні помилки без введення штучної надмірності.
Основне застосування коду Грея - передача інформації про процеси, що змінюються досить повільно. Числові значення характеристик таких процесів плавно переходять від одного до другого. Тому, якщо у даному повідомленні одночасно виявились зміненими декілька розрядів у порівнянні з попереднім повідомленням, то це означає наявність помилки.
Перші 16 кодів Грея представлено у таблиці:
| Число | Двійковий код | Код Грея | Число | Двійковий код | Код Грея |
Код Грея визначається індуктивно.
Для однорозрядного коду маємо два значення, які запишемо у стовпчик:
Утворимо двохрозрядний код. Під стовпчиком однорозрядних кодів запишемо такий же, тільки у протилежному порядку, і поставимо перед першим стовпчиком нулі, а перед другим - одиниці:
- - -
Видно, що при переході від першого стовпчика до другого змінюється лише тільки перший символ. І при переході між рядками теж змінюється тільки один символ. Крім того, останній та перший рядки також відрізняються одним першим символом.
Тепер утворимо трьохрозрядний код за такою ж самою схемою:
- - - -
Аналогічно можуть бути утворені коди Грея і з більшою розрядністю.
Розглянемо алгоритм перетворення двійкового числа у код Грея:
- перша одиниця зі сторони старших розрядів залишається без змін;
- кожна наступна цифра залишається без змін, якщо в утворюваному коді Грея їй передує парна кількість одиниць;
- кожна наступна цифра інвертується, якщо в утворюваному коді Грея їй передує непарна кількість одиниць.
Приклад: 1 1 0 0 1 0
1 0 1 0 1 1
Розглянемо алгоритм перетворення коду Грея у двійкове число:
- перша одиниця зі сторони старших розрядів залишається без змін;
- кожна наступна цифра залишається без змін, якщо у даному коді Грея їй передує парна кількість одиниць;
- кожна наступна цифра інвертується, якщо у даному коді Грея їй передує непарна кількість одиниць.
Приклад: 1 0 1 0 1 1
1 1 0 0 1 0
Тепер розглянемо перетворення коду Грея безпосередньо у десяткове число.
Пронумеруємо розряди коду Грея справа наліво, починаючи з одиниці. Вагою кожного одиничного розряду коду Грея є значення ±(2n-1), де n - номер цього розряду. Таким чином, вагами одиничних розрядів будуть слідуючі числа: ±1 при n=1, ±3 при n=2, ±7 при n=3, ±15 при n=4 і т.д. Ваги нульових розрядів коду Грея не розглядаються.
При перетворенні коду Грея в десяткове число знаки ваг для одиничних розрядів чергуються, починаючи зі знаку ‘+’, після чого додаються.
Приклад: 6 5 4 3 2 1 - номери розрядів;
1 0 1 0 1 1 - код Грея;
+63 -15 +3 -1 - ваги одиничних розрядів ® 50.
Поиск по сайту: