АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Системи числення

Читайте также:
  1. IV. Настільні видавничі системи.
  2. Афінська та спартанська системи виховання: порівняльний аналіз.
  3. АФО імунної системи
  4. АФО органів сечової системи
  5. Взаємодія користувача та файлової системи ПК
  6. Виборчі системи: їх ознаки та різновиди
  7. Виборчі системи: сутність І типологія
  8. Визначення неповних імунних антитіл системи AB0 непрямою пробою Кумбса
  9. Винагорода за працю. Заробітна плата: суть, форми і системи
  10. Випробування складальних одиниць гідросистеми
  11. Відновлення системи
  12. Відносин, який охоплює всю номенклатуру товарів. Тому реформа національної системи

 

У теорії інформації, кодування, передачі даних і система обміну інформацією найпоширенішими є двійкова, вісімковa та шістнадцяткова системи числення. Проте це ні в якому разі не означає, що на практиці не користуються іншими системами числення, такими як трійкова, четвіркова, шісткова тощо.

Узагалі ціле число N у будь-якій системі числення можна за­писати у вигляді ряду

N = 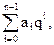(3.1)

де 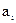– розрядні коефіцієнти, значення яких змінюються від І до q - 1;

q - основа (алфавіт) системи числення; i– номер роз­ряду; n – кількість їх.

Назва системи числення походить від основи (алфавіту) q: q = 2 – двійкова, q = 3 – трійкова, q = 8 – вісімкова систе­ми числення тощо.

Для запису чисел (табл. 3.1) у дев'ятковій системі використо­вують 10 цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9); у двійковій – дві (0 і 1); у трійковій – три (0,1,2); у вісімковій – вісім (0, 1, 2, 3, 4, 5, 6, 7), а в шістнадцятковій – 16 знаків, з них – 10 цифр (0...9) і шість літер (А, В, С, D, E, F).

Так, користуючись виразом (3.1), десяткове число 375 можна записати у вигляді ряду (375)10 = 3·102 + 7·101 + 5·10°.

Те саме число в двійковій системі числення запишеться як

(375)2 = 1 · 28 + 0 · 27 + 1 · 26 + 1 · 25 + 1· 24 + 0 · 23 + 1 · 22 + 1· 21 + 1 · 2°→ 101110111;

у трійковій- як

(375)3 = 1 · З5 + 1 · З4 + 1 · З3 + 2 · З2 + 2 · 3і + 0 · 3°→111220,

у вісімковій – як

(375)8 = 5 · 82 + 6· 81 + 7 · 8° → 567,

а в шістнадцятковій – як

(375)16 = 1 · 162 + 7 · 161 + 7 · 160→177.

Кількість комбінацій простого коду в будь-якій системі чис­лення залежить від алфавіту коду та довжини кодової комбіна­ції (N = qn) і, звичайно, чим більший алфавіт коду, тим менша кількість розрядів у комбінації.

Для запису десяткового числа в будь-якій системі числення треба поділити його на основу вибраної системи. Після першо­го ділення дістанемо цілу частку й остачу. Продовживши ді­лення цілої частки, матимемо нові цілу частку та остачу. Ді­лення цілих часток продовжуємо доти, доки частка не стане меншою від основи q системи числення. Ця остання частка й буде старшим розрядом числа у вибраній системі числення. Інші Розряди відповідатимуть остачам від ділення. Молодший роз­ряд – це остача від першого ділення.

 

Таблиця 3.1 – Представлення чисел у різних системах

Числа
десяткові двійкові вісімкові шістнадцяткові
       
       
       
       
       
б      
      7
       
       
      А
      В
      с
      D
      E
      F
       
       
       
       
       
       
       
       

 

Нехай число 217, записане в десятковій системі числення, треба пере­вести у двійкову систему. Виконуємо послідовне ділення числа 217 на 2 (в дужках зазначено остачі від ділення):

217:2= 108 +(1); 13:2 = 6 + 0);

108: 2 = 54 + (0); 6:2 = 3+ (0);

54: 2 = 27 + (0); 3:2=1+ (1);

27:2= 13+ (1); 1:2 = 0 + (1).

Відповідно до викладеного вище остання частка відділення, значення якої менше від основи системи числення (в даному разі це значення частки в передостанньому діленні, коли 1 < 2), є коефіцієнтом при основі систе­ми числення у найвищому степені (в даному разі це 1) або остання остача, що рівнозначно. Решта остач будуть коефіцієнтами при основі системи числення менших степенів. Таким чином, число 217 у двійковій системі числення записується у вигляді 11011001.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)