Способи подання кодів

Код кожного виду має свій найраціональніший спосіб по­дання, що випливає з його властивостей. Проте відомо також кілька загальних способів подання кодів, які є досить універ­сальними і можуть застосовуватися для опису широких кла­сів кодів. До цих способів належать подання кодів у вигляді:

1 таблиць кодових комбінацій;

2 кодового дерева;

3 геомет­ричної моделі;

4 матриці.

Перший спосіб полягає в поданні коду у вигляді таблиці всіх його комбінацій. Наприклад, п'ятиелементний двійковий бло­ковий код зі сталою вагою, в кожній комбінації якого містяться три одиниці, задається так:

Цей спосіб застосовується для подання будь-яких блокових кодів, але не може бути використаний для неперервних кодів.

Другий спосіб подання кодів полягає в зображенні комбінацій коду у вигляді кодового дерева, коли комбінації розміщуються в його вузлах. Під кодовим деревом розумітимемо графічний образ, який складається з точок і ліній, що розходяться від них i також закінчуються точками. Останні називатимемо вузлами, а лінії, які їх з'єднують, – ребрами. Перший вузол, від якого починається розходження ребер, називається коренем дерева, а

кількість ребер, які треба пройти від кореня до будь-якого вуз­ла –рівнем, або порядком, цього вузла.

Максимальна кількість вузлів, які зустрічаються під час руху вздовж кодового дерева в напрямку від кореня до вершини, визначає висоту h кодового дерева. Вона дорівнює максима­льній довжині комбінації коду, побудованому за допомогою цього дерева.

Вузли кодового дерева розташовуються на різних рівнях. Кожний рівень дерева рівномірного коду може мати qⁱ вузлів, де q – основа коду, i – номер рівня (i= 1 ,2,...,п, тут n – дов­жина коду). Для рівномірного двійкового простого коду кіль­кість вузлів на останньому рівні n дорівнює кількості N комбі­націй коду, тобто 2ⁿ= N.

Вузли, що не з'єднуються з наступними рівнями, називаються кінцевими; вони відповідають комбінаціям коду.

Основою коду обмежується максимальна кількість ребер, яка може виходити з кожного вузла дерева, а максимальною дов­жиною кодової комбінації – максимальна кількість рівнів ко­дового дерева. Кожному вузлу приписується значення розря­дів комбінації, що відповідає напрямкам руху вздовж ребер від кореня дерева до вузла. Ребра, що йдуть від кореня до вузлів першого рівня, визначають значення першого зліва розряду кодової комбінації, а ті, що з'єднують вузли першого та другого рівнів, – значення другого зліва розряду і т. д. На рис. 3.1 по­казано приклади кодових дерев: рівномірних двоелементного двійкового (рис. 3.1, α), двоелементного трійкового (рис. 3.1, б), триелементного двійкового (рис. 3.1, в) та нерівномірного двій­кового (рис. 3.1, г). Цей спосіб застосовується для зображення як блокових, так і неперервних кодів.

Рисунок 3.1 - Приклади кодових дерев

За допомогою кодових дерев легко зобразити префіксні коди, що мають властивість префікса й можуть бути утворені послі­довним викреслюванням останнього розряду кодової комбіна­ції, причому жодна з комбінацій даного префіксного коду не може бути префіксом його комбінації. Наприклад, префіксами кодової комбінації 10111001 будуть 1, 10, 101, 1011, 10111, 101110, 1011100, 10111001, тобто для однозначного її декоду­вання жодна з комбінацій цього коду не повинна мати перелі­чені вище комбінації.

Та частина, яка доповнює префіксний код до повної кодової комбінації, утворює суфікс, тобто кожна кодова комбінація складається з префікса та суфікса.

Префіксні коди можна утворити за допомогою кодового де­рева, в якого немає вершини і кожний його кінцевий вузол від­повідає комбінації префіксного коду.

Третій спосіб подання кодів полягає в зображенні комбіна­цій коду точками дискретного л-вимірного векторного просто­ру. Так, кожну комбінацію рівномірного блокового коду (з ос­новою q і довжиною n) V= (V_n, V_n-1,..., V₂, V₁) можна розглядати як вектор або точку деякого и-вимірного векторного простору з координатами V_n, V_n-1,..., V₂, V₁ Якщо значення q скінчен­не, а будь-яка координата вектора є цілим додатним числом від 0 до q - 1, то зазначений код можна розглядати як дискретний л-вимірний простір, що складається N = qⁿ точок, які відпові­дають кінцям усіх можливих векторів.

Цей л-вимірний простір дістав назву кодового. Кількість просторових вимірювань кодового простору для коду з будь-якою основою дорівнює довжині n коду, а кількість градацій по кожній з осей (напрямків вимірювання) визначається осно­вою коду і становить q - 1.

Якщо для дискретного n-вимірного простору, що тут роз­глядається, ввести поняття кодової відстані d між точками V_i та V_j, то матимемо

d(V_i, V_J) = (3.2)

Цілком природно, що для простору з відстанню (3.2), як і для будь-якого іншого кодового простору, d(V_i, V_J) = d(Vj,V_i).

Одним з основних параметрів коду з довільною основою q, що визначають його завадостійкість, є мінімальна кодова, відстань d_min. На відміну від кодової відстані d, що визначав кількість станів, які мають пройти якісні ознаки кодової ком­бінації, щоб опинитися в стані, який відповідає порівнюваній кодовій комбінації, мінімальна кодова відстань характеризує не дві окремо взяті комбінації, а код у цілому, і визначається мінімальною кількістю якісних ознак, за якими відрізняються одна від одної будь-яка пара комбінацій цього коду.

Для визначення кодової відстані між комбінаціями коду з основою q треба виконати їх порозрядне віднімання за моду­лем q. їздова відстань дорівнює вазі комбінації, що склада­ється з різниці значень комбінацій, між якими визначається ця відстань.

З'єднавши кожну точку простору, що розглядається, прями­ми лініями з усіма точками, віддаленими на відстань d(V_i, V_J) = 1, дістанемо геометричну фігуру сіткової структури. Цю фігуру називають геометричною моделлю n-елементного q-коду.

Точки дискретного простору, які містить ця геометрична фігура, називаються її вершинами, а лінії, що їх з'єднують, – ребрами.

На рис. 3.2 зображено геометричні моделі деяких кодів. Мо­деллю будь-якого двозначного набору якісних ознак (дво­елементного коду) є фігура двовимірного простору – квадрат (рис. 3.2, а) або фігура що складається з квадратів (рис. 3.2, б, д); моделлю будь-якого тризначного набору якісних ознак (триелементного коду)–фігура тривимірного простору–куб (рис. 3.2, в) або фігура, що складається з кубів (рис. 3.2, г, є).

Побудова моделі чотиризначного набору якісних ознак (чо­тириелементного коду), тобто фігури чотиривимірного прос­тору, можлива, якщо тривимірний куб або кожну з його вер­шин змістити в новому напрямку. Взагалі в цьому разі л-вимір­ний куб повинен мати 2n вершин, n∙ 2^n-1 ребер, n(n - 1) · 2^n-3 граней, а найвіддаленіша від певної його вершини точка має знаходитися на відстані л ребер.

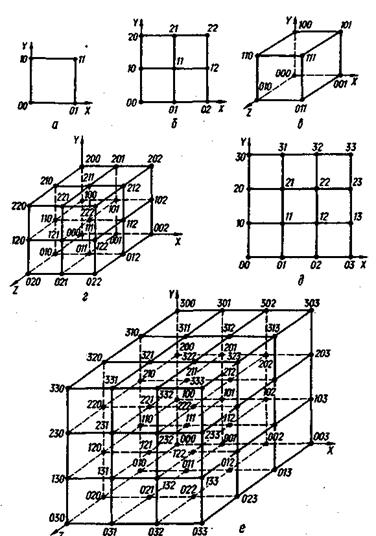
Рисунок 3.2 - Геометричні моделі деяких кодів

Розглянемо більш докладно властивості, що випливають з геометричної фігури, яка є моделлю л-елементного двійкового коду й дістала назву n-вимірного куба. Відстань між будь-яки­ми його вершинами, тобто між двома кодовими комбінаціями, згідно з (3.2) можна визначити як кількість розрядів, якими вони різняться. Так, відстань між комбінаціями 010 і 100 дорівнює двом, оскільки вони різняться елементами в двох розрядах – першому та другому.

Відмінність елементів однойменних розрядів комбінацій двій­кового коду легко визначити, застосувавши до них операцію Додавання за модулем 2. Як відомо, результат такого додавання тільки тоді дорівнює 1, коли числа, що додаються, різняться. З урахуванням цього відстань між будь-якими двома комбінаціями n-елементного двійкового коду (вершинами n-вимірного куба) визначається виразом

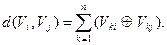(3.3)

Відстань між комбінаціями V_i та V_j можна знайти також че­рез кількість одиниць у деякій комбінації V_l [або через її вагу w(V_l) ], здобуту після додавання за модулем 2 комбінацій V_i та V_j(V_l= V_i V_j):

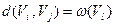. (3.4)

Зручність геометричної моделі зображення будь-якого коду полягає в тому, що кожна її вершина відповідає одній комбіна­ції коду, а відстань між комбінаціями V_i та V_j згідно з (3.2) дорів­нює кількості ребер, які треба пройти найкоротшим шляхом з вершини V_i до вершини Vj.

Недоліком геометричної моделі є те, що при довжині коду n > З зобразити її у звичайному тривимірному просторі немож­ливо. Тому вона застосовується лише для рівномірних блокових кодів з метою наочного зображення та полегшення аналізу їх­ніх властивостей.

Четвертий спосіб подання кодів у вигляді матриці з 2ⁿ ряд­ками та n стовпцями можливий тільки для рівномірних n-елементних двійкових блокових кодів. Якщо матрицею подається сукупність ненульових комбінацій коду, то кількість рядків дорівнюватиме 2ⁿ - 1.

З урахуванням того, що матриця л-елементного коду склада­ється з 2ⁿ - 1 комбінацій, записаних у вигляді рядків, особли­вість такого запису полягає в тому, що додавання за модулем 2 будь-якої кількості рядків цієї матриці приводить до появи дозволеної комбінації коду, в тому числі й нульової. Якщо останню відкинути, то дістанемо нову матрицю коду, але вже з меншою кількістю рядків. Повторивши аналогічну операцію додавання рядків матриці за модулем 2, можна знову дістати нульову комбінацію коду. Ця операція повторюється доти, поки не буде здобута матриця з лінійно незалежними рядками, до­давання яких за модулем 2 вже не приведе до утворення нульо­вої комбінації коду.

Наприклад, щоб побудувати матрицю триелементного двій­кового простого коду, треба, записавши у вигляді матриці всі 2ⁿ - 1 комбінацій простого коду, крім нульової, послідов­но додати їх за модулем 2, виключаючи кожного разу ті ком­бінації, які в сумі з попередніми утворюють нульову комбі­націю:

Друга колонка тут формується так: якщо до третього рядка першої колонки додати суму її першого та другого рядків, то утвориться нульова комбінація, яку виключаємо при запису третьої колонки. Якщо до п'ятого рядка другої колонки після цього додати суму її першого та четвертого рядків, то дістане­мо нульову комбінацію в третій колонці. Цю комбінацію та­кож виключаємо, записуючи четверту колонку, і т. д. Таким чином, відкинувши всі нульові комбінації, матимемо шосту колонку з кодовими комбінаціями, що містять тільки по одній одиниці. Це й буде матриця даного коду (сьома колонка).

Квадратна матриця, діагональ якої складається з одиниць, а решта її елементів – нулі, називається одиничною. Якщо рядки такої n-елементної матриці додавати за модулем 2, то підбо­ром відповідної комбінації їх можна дістати всі комбінації л-елементного коду. Тому такі матриці ще називаються визна­чальними.

Якщо напрямок головної діагоналі матриці проходить справа наліво, то матриця називається транспонованою. Для розгля­нутого коду це буде матриця (шоста колонка)

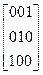
Загалом визначальна матриця n-елементного коду записується так:

n рядків

n стовпців

Розглянутий приклад утворення визначальної матриці й здо­бута одинична матриця можуть бути використані тільки для побудови всіх комбінацій двійкового простого коду з мінімаль­ною кодовою відстанню d_min - 1.

Матричний спосіб може бути застосований також для побу­дови коректувальних кодів з d_min > 1, здатних виявляти та вип­равляти помилки. Проте при цьому твірна (породжувальна) матриця складається з двох підматриць – уже відомої одинич­ної (інформаційної) та додаткової (перевірної).

За допомогою інформаційної одиничної підматриці Е_k утво­рюють інформаційну частину кодової комбінації коректуваль­ного коду, яка складається з k інформаційних елементів і визна­чає розмір підматриці (k x k:), що відповідає розмірам визначаль­ної квадратної матриці двійкового простого коду, оскільки кіль­кість N комбінацій коректувального коду дорівнює кількості N комбінацій початкового двійкового простого коду, які тре­ба закодувати цим коректувальним кодом.

За допомогою додаткової перевірної підматриці С_r,k, утворюють перевірну частину комбінації ко­ректувального коду, що складається з r перевірних елементів. Тому додаткова перевірна підматриця має розмір r x k.

Таким чином, загальний розмір твірної матриці коректуваль­них кодів дорівнює n x k, оскільки n = k + r.

Поиск по сайту: