 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
СТАТИСТИЧЕСКИХ ГИПОТЕЗ И
ДИСПЕРСИОННОГО АНАЛИЗА
ПРИ ПОМОЩИ EXCEL»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторной работе
по дисциплинам «Прикладная статистика»
для студентов специальностей:
для студентов специальностей:
7.050201 – «Менеджмент организаций»,
7.050104 – «Финансы»
7.050106 – «Учет и аудит»
7.050107 – «Экономика предприятия»
всех форм обучения
Севастополь
УДК 681.5.015.:330.43
«Выполнение проверки статистических гипотез и дисперсионного анализа при помощи Excel» методические указания к лабораторной работе по дисциплине «Прикладная статистика» для студентов специальностей: 7.050201 – «Менеджмент организаций», 7.050104 – «Финансы», 7.050106 – «Учет и аудит», 7.050107 – «Экономика предприятия» всех форм обучения / Сост. А.А. Загорулько, А.Д. Горобец. – Севастополь: Изд-во СевНТУ, 2007г. – 16с.
Целью методических указаний является закрепление теоретических знаний и приобретение практических навыков по темам «Проверка статистических гипотез» и «Дисперсионный анализ» при решении ситуаций с помощью Excel. Методические указания предназначены для студентов экономических специальностей всех форм обучения.
Методические указания утверждены на заседании кафедры менеджмента и экономико-математических методов, (протокол № 7 от «16»марта 2007г.)
Допущено учебно-методическим центром СевНТУ в качестве методических указаний
Рецензент: Одинцова Т.М., канд. эконом. наук, доцент кафедры «Финансы и кредит»
СОДЕРЖАНИЕ
1. Цель работы.............................................................................4
2.Теоретическая часть..................................………………………..4
2.1. Проверка статистических гипотез...............…………………………4
2.2. Проверка статистических гипотез в Excel......................................5
2.3. Дисперсионный анализ..............................................................7
2.4. Выполнение дисперсионного анализа в Excel…………………………..8
3.Варианты заданий...................................................................12
3.1. Варианты заданий по теме «Проверка статистических гипотез»………………………………………………………………………12
3.2. Варианты заданий по теме «Однофакторный дисперсионный анализ»……………………………………………………………………….13
4. Содержание отчета.................................................................14
5. Контрольные вопросы............................................................14
Библиографический список.......................................................15
ЦЕЛЬ РАБОТЫ
Данные методические указания предназначены для закрепления теоретических знаний и получения практических навыков студентов при проверке статистических гипотез и выполнении дисперсионного анализа в Excel.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
2.1. Проверка статистических гипотез
Статистическая гипотеза - некоторое предположение о законе распределения случайной величины или о параметрах этого закона в рамках данной выборки.
Пример статистической гипотезы: «генеральная совокупность распределена по нормальному закону», «различие между дисперсиями двух выборок незначимо» и т.д.
При аналитических расчетах часто необходимо выдвигать и проверять гипотезы. Проверка статистической гипотезы осуществляется с помощью статистического критерия в соответствии со следующим алгоритмом:
1) формулировка гипотезы. Гипотеза формулируется в терминах различия величин. Например, есть случайная величина х и константа a. Они не равны (арифметически), но нужно установить, значимо ли статистически между ними различие. Существует два типа критериев:
а) двухсторонний критерий вида: х 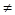 a;
a;
б) односторонний критерий вида: х< a или х< a.
Необходимо отметить, что знаки >, <, = здесь используются не в арифметическом, а в «статистическом» смысле. Их необходимо читать «значимо больше», «значимо меньше», «различие незначимо».
2) Установка закона распределения. Далее необходимо установить или постулировать закон распределения. Существуют также критерии, которые не зависят от вида распределения - так называемые непараметрические критерии.
3) Вычисление тестовой статистики. Тестовая статистика - некоторая функция от рассматриваемых величин, закон распределения которой точно известен и ее можно сравнить с табличным значением.
4) Сравнение с табличным значением. Затем тестовая статистика сравнивается с табличным значением. Тестовая статистика всегда зависит от доверительной вероятности, и, в некоторых случаях, от дополнительных параметров. Так, в приведенном выше примере сравнения двух дисперсий тестовая статистика сравнивается с табличным значением критерия Фишера («критическим» значением), которое зависит от доверительной вероятности и числа степеней свободы дисперсий.
5) Вывод. На основании сравнения делается вывод о том, выполняется ли гипотеза (например, значимо ли различие и т.д.).
2.2. Проверка статистических гипотез в Excel
Рассмотрим пример.
Туристическая фирма в среднем реализует 21 путевку в страны ближнего зарубежья в день. Количество проданных путевок за последнюю неделю составило: 17, 19, 25, 32, 27, 30, 28. Полагая, что уровень значимости равен 5% определить:
- выполняет ли компания план по продаже путевок в страны ближнего зарубежья;
- увеличился ли среднего ежедневного объема продаж путевок за последнюю неделю.
Для выполнения проверки статистических гипотез в Excel необходимо произвести расчеты и вычислить значение критерия Стьюдента.
Решение.
На первом этапе выдвигаются нулевая и альтернативная гипотезы:
H0: 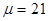
H1:  .
.
После чего необходимо определить табличное значение критерия Стьюдента. Для этого в меню «Вставка» выбирается команда «Функция». Устанавливается категория «Статистические» и выбирается функция «СТЬЮДРАСПРОБР». Пример заполнения окна для определения табличного значения критерия Стьюдента представлен на рисунке 1.
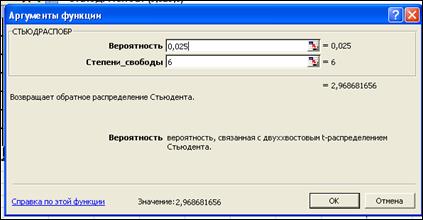
Рисунок 1 – Пример заполнения окна для определения табличного значения критерия Стьюдента
В поле «Вероятность» вводится заданный уровень значимости (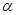 ), а так как альтернативная гипотеза имеет следующий вид: H1:
), а так как альтернативная гипотеза имеет следующий вид: H1:  , то необходимо применять двусторонний тест. При использовании двустороннего теста вместо значения
, то необходимо применять двусторонний тест. При использовании двустороннего теста вместо значения 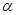 берется значение
берется значение 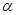 /2 (для рассматриваемого примера
/2 (для рассматриваемого примера 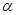 /2=0,025).
/2=0,025).
В поле «Степени свободы» вводится значение, равное n-1, где n- число элементов в выборке (для рассматриваемого примера n-1=6).
В результате мы определили, что табличное значение критерия Стьюдента для данной задачи равно 2,968.
Правило принятия (отвержения) гипотезы: если TR<-2,968 и TR>2,968, то отвергается H0 и принимается H1.
Далее необходимо выполнить следующие вычисления:
Вычисление t расчетного (TR) производиться по следующей формуле:
 , (1)
, (1)
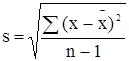 . (2)
. (2)
Таблица 1 - Промежуточные вычисления
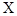
| 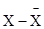
| 
|
| -8,43 | 71,0649 | |
| -6,43 | 41,3449 | |
| -0,43 | 0,1849 | |
| 6,57 | 43,1649 | |
| 1,57 | 2,4649 | |
| 4,57 | 20,8849 | |
| 2,57 | 6,6049 | |
| 185,7143 |
Таким образом имеем:
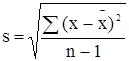 =
= 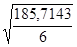 =5,563
=5,563
 =
= 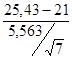 =2,11
=2,11
На заключительном этапе происходит принятие статистического решения.
Так как -2,968<TR<2,968, тогда с  =0,05 гипотеза Н0 о равенстве среднего значения количества проданных путевок за день в размере 21 штуки принимается. Следовательно, туристическая компания выполняет план по продаже путевок в страны ближнего зарубежья.
=0,05 гипотеза Н0 о равенстве среднего значения количества проданных путевок за день в размере 21 штуки принимается. Следовательно, туристическая компания выполняет план по продаже путевок в страны ближнего зарубежья.
При ответе на второй вопрос задания нулевая и альтернативная гипотеза будут иметь вид:
H0: 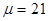
H1: 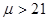 .
.
Так как альтернативная гипотеза имеет следующий вид: H1: 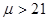 , то необходимо применять односторонний тест. При использовании одностороннего теста табличное значение критерия Стьюдента определяется таким же образом, как и для двустороннего теста, но в поле «Вероятность» указывается значение
, то необходимо применять односторонний тест. При использовании одностороннего теста табличное значение критерия Стьюдента определяется таким же образом, как и для двустороннего теста, но в поле «Вероятность» указывается значение 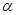 (для рассматриваемого примера
(для рассматриваемого примера 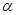 =0,05). Таким образом, табличное значение критерия Стьюдента для одностороннего теста равно 2,446.
=0,05). Таким образом, табличное значение критерия Стьюдента для одностороннего теста равно 2,446.
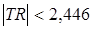 , то принимается гипотеза H0 о равенстве среднего значения количества проданных путевок в размере 21 штуки в день при
, то принимается гипотеза H0 о равенстве среднего значения количества проданных путевок в размере 21 штуки в день при 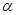 =0,05. Следовательно, нельзя говорить об увеличении среднего ежедневного объема продаж путевок за последнюю неделю.
=0,05. Следовательно, нельзя говорить об увеличении среднего ежедневного объема продаж путевок за последнюю неделю.
2.3 Дисперсионный анализ
Дисперсионным анализом называют статистический метод анализа результатов, зависящих от действия количественных или качественных факторов. Включает в себя проверку гипотез, связанных с оценкой выборочной дисперсии. Может показаться странным, что процедура сравнения средних называется дисперсионным анализом. В действительности, это связано с тем, что при исследовании статистической значимости различия между средними двух (или нескольких) групп, сравниваются (анализируются) выборочные дисперсии. Фундаментальная концепция дисперсионного анализа предложена Фишером в 1920 году
Дисперсионный анализ может быть использован для выявления совместного влияния экономических факторов, неподдающихся количественному измерению, на изучаемый показатель. Суть метода в том, что общая вариация результирующего показателя расчленяется на части, соответствующие раздельному и совместному влиянию различных качественных факторов, и остаточную вариацию, аккумулирующую влияние всех неучтенных факторов. Статистическое изучение этих частей позволяет делать выводы о том, действительно ли оказывает влияние на результирующий показатель тот или иной фактор.
Можно выделить три основных вида гипотез:
1)  =
= 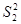 (значимо ли различие между двумя дисперсиями?);
(значимо ли различие между двумя дисперсиями?);
2)  >
> 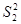 (одна дисперсия значимо больше другой?);
(одна дисперсия значимо больше другой?);
3)  =
= 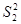 =…=
=…= 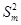 (значимо ли различие между несколькими дисперсиями?).
(значимо ли различие между несколькими дисперсиями?).
Дисперсия вычисляется из случайных величин, и поэтому сама также является случайной величиной. Дисперсии, в отличие от средних, подчиняются распределению 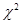 .
.
Первые две гипотезы дисперсионного анализа проверяются с помощью критерия Фишера. Причем первая гипотеза - с помощью двустороннего критерия, а вторая - с помощью одностороннего. Строго говоря, эти критерии не равны, но в общем случае разницей можно пренебречь. Проверка производится по следующей формуле:
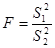 (3)
(3)
С третьей гипотезой (сравнение нескольких дисперсий или проверка однородности дисперсий) дело обстоит сложнее. Попарно сравнивать дисперсии некорректно. В дисперсионном анализе для сравнения нескольких дисперсий существует два критерия: критерий Бартлетта и критерий Кохрена.
2.4 Выполнение дисперсионного анализа в Excel
Рассмотрим дисперсионный анализ на следующем примере: за месяц известны данные о выработке рабочего за время работы в первую и во вторую смены.
Таблица 2 - Исходные данные
| Смена | Выработка рабочего, нормо-час |
| 12,1; 11,1; 12,6; 12,9; 11,6; 13,1; 12,6; 12,4; 11,6; 17,3; 12,9; 11,6; 12,4 | |
| 9,9; 11,4; 13,4; 10,4; 12,9; 12,6; 13,9; 13,4; 12,4; 9,9; 10,2; 11,2; 9,7 |
Можно ли считать, что расхождение между уровнями выработки рабочего в первую и во вторую смены несущественно, т.е. можно ли считать, что генеральные средние в двух подгруппах одинаковы и, следовательно, выработка рабочего может быть охарактеризована общей средней.
Решение.
Для того чтобы ответить на поставленные вопросы, рассчитаем среднюю выработку рабочих в каждой смене. Величина выработки в первую и вторую смены различна. Теперь возникает вопрос о том, насколько существенны эти расхождения, нужно проверить предположение о возможном влиянии сменности на выработку рабочих. Результаты расчетов сведены в таблицу 3.
Таблица 3 – Промежуточные расчеты для проведения дисперсионного анализа
| Смена | Средняя выработка, нормо-часы
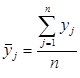
| Число смен в месяце
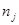
| Сумма квадратов отклонений вариантов от групповой средней

| Квадраты отклонений групповых средних от общей средней
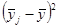
|
| 12.63 | 28.0877 | 0.2461 | ||
| 11.63 | 28.0707 | 0.2461 | ||
| Итого | 
| 56.1584 |
Используя данные графы 4 и графы 5, рассчитаем  и
и 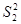 .
.
Число степеней свободы для расчета внутригрупповой дисперсии равно 24 (26-2), а для расчета межгрупповой дисперсии число степеней свободы равно 1 (2-1).
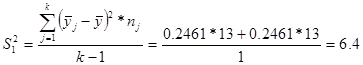
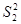 =
= 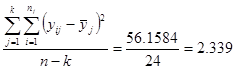
Рассчитаем значение критерия Фишера по следующей формуле:
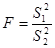 (4)
(4)
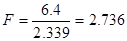
В соответствии с числом степеней свободы для расчета внутригрупповой и межгрупповой дисперсий (24 и 1) в таблице F-распределения для α=5% находим Fтабл = 4.26.
При этом выдвигается две гипотезы. Нулевая гипотеза гласит о том, что различия выработки рабочего в первую и вторую смены несущественны. Альтернативная гипотеза: существуют существенные различия в значении выработки рабочего в первую и во вторую смены.
Так как расчетное значение критерия Фишера значительно меньше табличного значения критерия Фишера, то гипотеза о несущественности различия выработки рабочего в первую и вторую смены не опровергается, т.е. сменность не оказывает влияния на уровень выработки рабочего.
Выполнение однофакторного дисперсионного анализа в Excel.
Для того, чтобы провести дисперсионный анализ в Excel, необходимо активировать команду «Анализ данных». Для этого проходится следующий путь: Сервис -> Надстройки -> Пакет анализа. После этого в меню «Сервис» появляется команда «Анализ данных» и выбирается команда «Однофакторный дисперсионный анализ».
Далее необходимо заполнить окно «Анализ данных»:
«Входной интервал» - вводится ссылка на диапазон, содержащий анализируемые данные. Ссылка должна состоять не менее чем из двух смежных диапазонов данных, данные в которых расположены по строкам или столбцам.
«Группирование» - установите переключатель в положение. По столбцам или По строкам в зависимости от расположения данных во входном диапазоне.
«Метки в первой строке/Метки в первом столбце» - если первая строка исходного диапазона содержит названия столбцов, установите переключатель в положение Метки в первой строке. Если названия строк находятся в первом столбце входного диапазона, установите переключатель в положение Метки в первом столбце. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически.
«Альфа» - введите уровень значимости, необходимый для оценки критических параметров F-статистики. Уровень альфа связан с вероятностью возникновения ошибки типа I (опровержение верной гипотезы).
«Выходной диапазон» - введите ссылку на левую верхнюю ячейку выходного диапазона. Размеры выходной области будут рассчитаны автоматически, и соответствующее сообщение появится на экране в том случае, если выходной диапазон занимает место существующих данных или его размеры превышают размеры листа.
«Новый лист» - установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.
«Новая книга» - установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.
Поиск по сайту: