АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Сила поля равна со знаком минус градиенту потенциальной энергии в данной точке поля

Читайте также:
  1. IV. Современные методы синтеза неорганических материалов с заданной структурой
  2. А.) Значение Психической Энергии
  3. Абсолютно упругий и неупругий удар тел. Внутренняя энергия. Общефизический закон сохранения энергии
  4. Автоматизированные системы контроля и учета электроэнергии (АСКУЭ).
  5. Аксиома о потенциальной опасности деятельности
  6. Активные потери энергии в аппаратах
  7. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
  8. Аналитический подход к исследованию величин в критической точке
  9. Апрель 2011. За несколько дней до знакомства с Скарлетт. Взято из воспоминаний Найла и Гарри.
  10. Белорусское искусство XVIII века. График Гершка Лейбович, резчик Ян Шмитт, художники Хеские. Слуцкие пояса и другие произведения декоративно-прикладного искусства данной эпохи.
  11. БОЛЕЗНЕТВОРНОЕ ДЕЙСТВИЕ ТЕПЛОВОЙ ЭНЕРГИИ. ПЕРЕГРЕВАНИЕ. ТЕПЛОВОЙ УДАР
  12. Боязнь незнакомых людей, страх отделения и привязанность

 

Представим себе, что мы имеем систему материальных точек. Пусть в этой системе действуют только консервативные силы. Тогда для каждой из материальных точек справедливо:

; ; , где 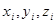- координаты - ой материальной точки.

Назовем: 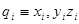- обобщенная координата - ой материальной точки.

Тогда .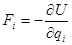

В состоянии равновесия все силы в системе должны обращаться в нуль, так как наличие силы означает ускорение какой-либо материальной точки, т.е. отсутствие равновесия. Следовательно, в состоянии равновесия все .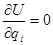

Однако это – условие экстремума потенциальной энергии: система будет находиться в равновесии, если ее потенциальная энергия минимальна (устойчивое равновесие) или максимальна (неустойчивое равновесие).

Если в системе не действуют диссипативные силы, то она находится в равновесии при условии, что ее потенциальная энергия экстремальна.

 

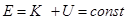- полная энергия в изолированной системе постоянна.

 

Работа Þ приращение кинетической энергии и убыль потенциальной.

 

 


2 Лекция 2


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)