Примеры консервативных сил

Пример 1. Сила упругости .

Пример 2. Гравитационная (или кулоновская сила)

, - гравитационная,

- кулоновская.

.

Работа этой силы на пути 1-2:

.

Пример 3. Сила тяжести:

РИС. 2-12

( - ускорение свободного падения, - единичный орт),

;

.

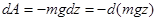Работа силы на пути 1-2:

.

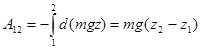Легко видеть, что каким бы способом мы ни выбирали точки 1 и 2, работа сил тяжести будет определяться только разностью «высот» этих точек и ничем более.

Следовательно, работа силы тяжести не зависит от формы пути, а определяется только начальным и конечным положениями перемещающейся точки.

Центральные силы

Сила называется центральной, если она направлена к одной и той же точке (или от нее) и зависит только от расстояния до этой точки, называемой силовым центром.

Таковы сила гравитации, кулоновская сила.

Запишем ; - проекция элементарного перемещения на направление силы º проекция на направление радиуса
Þ .

, причем следует еще раз подчеркнуть, что сила зависит только от абсолютного значения .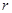

Полная величина работы определяется, следовательно, как

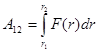- значение этого интеграла зависит только от расстояний и , но не от пути между и . В эту формулу путь перехода просто-напросто не входит, в нее входит только расстояние до силового центра.

Очевидно также, что при учете перемещения силового центра (в предыдущих рассуждениях мы полагали силовой центр неподвижным) мы получим тот же результат.

Действительно, в этом случае мы должны рассмотреть систему, составленную из двух частиц. Работа в системе аддитивна:

.

В соответствии с третьим законом Ньютона

.

Отсюда:

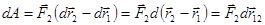( - взаимное расстояние точек).

Отсюда следует, что любую из рассматриваемых точек можно считать неподвижной, а другую перемещаемой.

Вывод: все центральные силы (и сила тяжести) являются силами консервативными.

Работа консервативных сил по замкнутому пути

Поиск по сайту: