 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент количества движения в системе материальных точек
Для системы материальных точек справедливо:
для моментов импульса и сил
 и
и 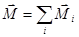 (
( - момент всех сил,
- момент всех сил,  - моменты отдельных сил).
- моменты отдельных сил).
Последнее следует из:
 :
:
Используя векторное умножение слева и справа на 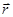 , находим:
, находим:
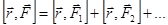 Þ
Þ 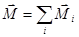 .
.
Под  следует понимать момент, создаваемый в системе всеми силами, как внешними, так и внутренними.
следует понимать момент, создаваемый в системе всеми силами, как внешними, так и внутренними.
Теорема. Полный момент внутренних сил, действующих в системе материальных точек, относительно любого полюса всегда равен нулю.
Доказательство
Внутренние силы всегда действуют попарно: силе 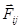 , с которой материальная точка
, с которой материальная точка 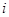 действует на материальную точку j, всегда соответствует равная и противоположно направленная сила
действует на материальную точку j, всегда соответствует равная и противоположно направленная сила  , с которой точка (частица) j действует на точку i, причем обе эти силы направлены вдоль одной прямой.
, с которой точка (частица) j действует на точку i, причем обе эти силы направлены вдоль одной прямой.
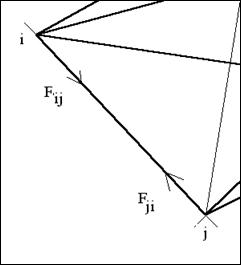
РИС. 3-8
 Вспомогательная теорема
Вспомогательная теорема
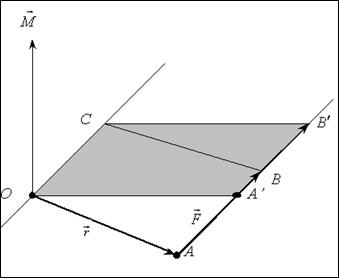
Момент силы  не изменится, если точку приложения силы
не изменится, если точку приложения силы 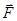 перенести в любую другую точку, расположенную на линии действия силы.
перенести в любую другую точку, расположенную на линии действия силы.
РИС. 3-9
Доказательство
Так как  , то
, то  равняется площади OABC. Площади OABC и OA’B’C равны, так как они имеют общее основание OC и высоту – что требовалось доказать.
равняется площади OABC. Площади OABC и OA’B’C равны, так как они имеют общее основание OC и высоту – что требовалось доказать.
Отсюда следует: равные силы 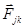 и
и 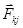 можно перенести в одну точку, где они друг друга скомпенсируют. Следовательно, полный момент внутренних сил равен нулю.
можно перенести в одну точку, где они друг друга скомпенсируют. Следовательно, полный момент внутренних сил равен нулю.
Обобщение
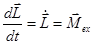 - производная по времени момента количества движения системы материальных точек относительно произвольного неподвижного полюса равна геометрической сумме моментов всех внешних сил относительно того же полюса.
- производная по времени момента количества движения системы материальных точек относительно произвольного неподвижного полюса равна геометрической сумме моментов всех внешних сил относительно того же полюса.
Следовательно, если момент внешних сил относительно неподвижного начала равен нулю, то момент количества движения (момент импульса) системы материальных точек относительно того же начала остается постоянным во времени.
Закон сохранения момента количества движения:
 ;
;  (не изменяется ни величина, ни направление)
(не изменяется ни величина, ни направление)
Момент количества движения в случае центральных сил
Поиск по сайту: