РЕШЕНИЕ. 1. Вычисляем коэффициенты

1. Вычисляем коэффициенты 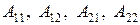. В соответствии с формулами (54), получаем:

2. Составляем приближённое уравнение изогнутой поверхности срединного слоя. Подставляя значения приведённых коэффициентов 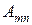в выражение (а), будем иметь:

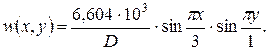(б)

3. Определяем внутренние усилия. На основании соотношений (55)–(57), находим:

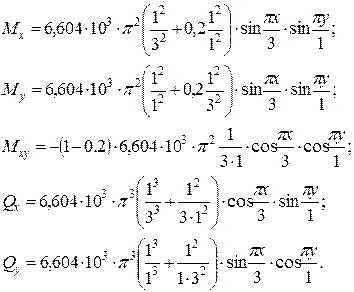(в)

4. Строим эпюры прогибов и изгибающих моментов по точкам в сечении и в сечении . На основании соотношений (в), получим:

- сечение :

- сечение :

Соответствующие графики представлены на рис. 20.

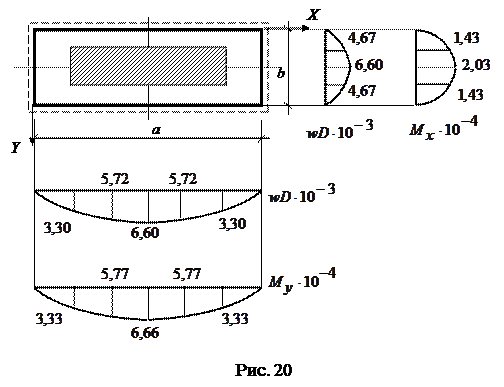Вычисления прогибов и изгибающих моментов сведены в табл. 12.

Таблица 12

5. Подбираем толщину пластины. Из эпюр изгибающих моментов следует, что самые большие моменты, а, следовательно, в соответствии с формулами (36) и самые большие нормальные напряжения и возникают в центре пластины на верхней и нижней её поверхности.

В силу симметрии крутящий момент в центре пластины и, следовательно, . Таким образом, в наиболее опасной точке имеем плоское напряженное состояние и напряжения и являются главными нормальными напряжениями. Поскольку и , то знак у напряжений и будет определяться знаком координаты (см. формулы (36)), то есть на верхней грани пластины оба напряжения будут положительными, на нижней – отрицательными. Учитывая значение моментов и в точке , получаем: и поскольку, как известно, и для пластин .

В соответствии с теорией прочности Треска–Сен-Венана (14) , толщина пластинки будет определяться по формуле

. (г)

Отсюда находим минимальную толщину пластины:

. (д)

В соответствии с теорией прочности Губера-Мизеса-Генки (16) 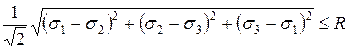, толщина пластины будет определяться по формуле:

, и будет равна

. (е)

В качестве расчётной толщины плиты принимаем .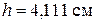

6. Определяем распределённые реакции. На основании соотношений (58) получаем

1)

2)

3)

4)

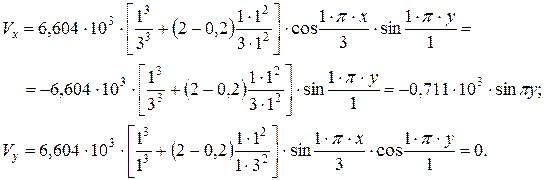
7. Строим эпюры распределённых реакций. В соответствии с полученными формулами для приведённых поперечных сил и строим эпюры распределённых реакций по точкам (рис. 21). Вычисления показывают, что распределённые реакции вдоль контура пластины направлены вверх и одинаковы на противоположных сторонах пластины. Результаты вычислений сведены в табл. 13.

Таблица 13

8. Определяем сосредоточенные реакции в углах пластины. На основании формул (59)-(62), получаем:

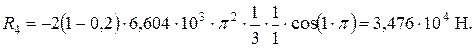
Все четыре реакции направлены вниз (рис. 21), то есть в сторону действующей нагрузки. Это значит, что углы пластины стремятся сместиться вверх и их нужно специальным образом закреплять от подъёма.

Решение задачи с использованием математического пакета MathCAD

Ниже, в качестве иллюстративного примера, представлено решение задачи подбора толщины тонкой пластины в среде математического пакета MachCAD. Эта часть контрольной работы является не обязательной для выполнения. Студент вправе самостоятельно выбрать способ решения задачи: либо решать задачу в режиме ручного счёта, либо решать задачу с использованием возможностей математического пакета MachCAD.

При решении задачи в среде математического пакета MathCAD следует иметь в виду, что, поскольку с самого начала значение цилиндрической жёсткости 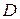неизвестно (так как неизвестна толщина пластины ), то весь расчёт строится в величинах, приведённых к цилиндрической жёсткости. Так, по формулам (54) вычисляются приведённые к цилиндрической жёсткости коэффициенты ряда Фурье: . Единицей измерения полученных величин будет . В силу этого и прогибы, вычисляемые через приведённые к цилиндрической жёсткости коэффициенты ряда Фурье, то есть приведённые к цилиндрической жёсткости, в соответствии с выражением (47) будут измеряться в . Приведённые к цилиндрической жёсткости изгибающие и крутящий моменты, также вычисляемые через приведённые к цилиндрической жёсткости коэффициенты ряда Фурье, в соответствии с формулами (55), (56), будут измеряться в ньютонах . Соответственно приведённые к цилиндрической жёсткости поперечные силы (формулы (57)) и распределённые реакции будут измеряться в . Сосредоточенные реакции в углах пластины (формулы (59)-(62)), приведённые к цилиндрической жёсткости, будут измеряться в ньютонах .

Решение задачи подбора толщины тонкой пластины с использованием возможностей математического пакета MathCAD представлено ниже.

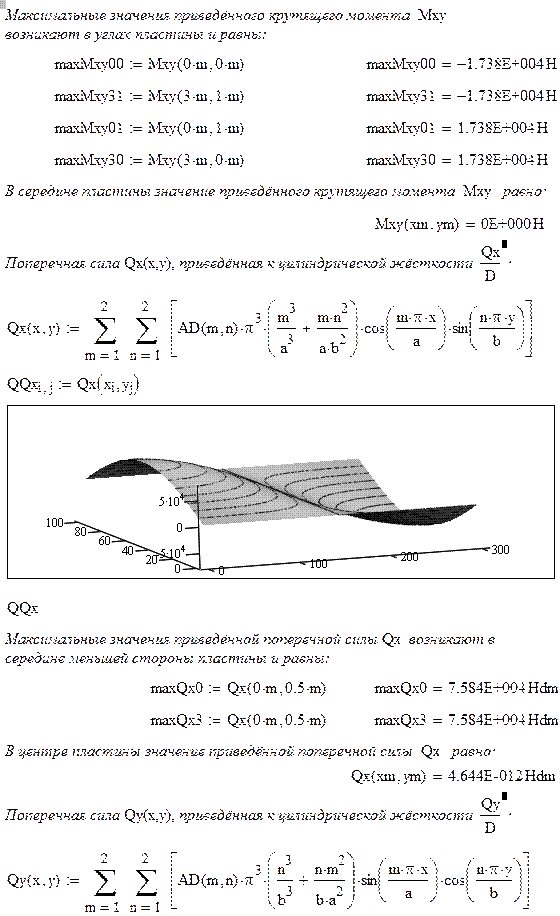
Таким образом, подбор толщины пластины шарнирно опёртой по всем сторонам и нагруженной равномерно распределенной нагрузкой симметричной относительно осей, проходящих через центр пластины параллельно её сторонам, сводится к определению максимальных значений изгибающих моментов и . В случае неравномерной нагрузки, несимметричной относительно её “центральных осей”, задача подбора толщины пластины значительно усложняется, поскольку, строго говоря, сводится к нахождению такой точки , в которой нарушается принятое условие прочности. Несколько проще решить задачу проверки прочности пластины с заданными геометрическими размерами (длиной, шириной и высотой).

Ниже, в качестве примера, приводится задача проверки прочности пластины, реализованная в среде математического пакета MathCAD. Пластина имеет шарнирное опирание по всем сторонам и нагружена равномерно распределённой нагрузкой по площади ABCD, смещённой к левому заднему углу пластины (рис. 22).

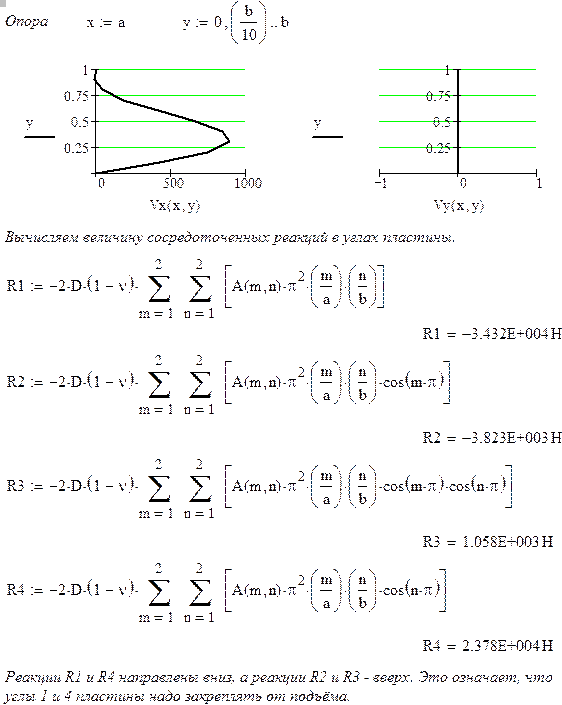
На рис. 23 показаны эпюры распределённых реакций, возникающие на шарнирных опорах пластины и сосредоточенные реакции в углах пластины, загруженной равномерно распределённой нагрузкой в первой четверти площади (рис. 22).

Контрольные вопросы.

1. Какие пластины называются тонкими?

2. Сформулируйте основные допущения, принятые в технической теории изгиба тонких пластин.

3. Что называется срединной плоскостью пластины при изгибе?

4. Чем отличается изгиб пластины от изгиба балки?

5. Какие внутренние усилия возникают в поперечных сечениях пластины при изгибе?

6. Что называется погонным усилием?

7. Какие напряжения возникают в поперечных сечениях пластины, и как они распределяются по высоте сечения? (Покажите эпюры напряжений.)

8. Как связаны между собой напряжения и прогибы срединной плоскости пластины при её изгибе?

9. Как найти напряжения в пластине по известным погонным внутренним усилиям?

10. Как определяются максимальные напряжения в пластине?

11. Какой вид напряжённого состояния имеет место в верхних и нижних волокнах пластины и почему?

12. Сформулируйте критерий прочности Губера-Мизеса-Генки для пластины.

13. Что такое погонный момент инерции?

14. Что такое погонный момент сопротивления?

15. Что такое цилиндрическая жёсткость?

16. Запишите дифференциальное уравнение изогнутой поверхности пластины.

17. Что понимается под граничными условиями и зачем они нужны при расчёте пластин?

18. Как записываются граничные условия для пластины, жёстко заделанной по контуру?

19. Как записываются граничные условия для пластины с шарнирным опиранием по контуру?

20. Как записываются граничные условия для пластины со свободным опиранием по контуру?

21. Как записать граничные условия для пластины, у которой одна сторона имеет жёсткое опирание, противоположная – шарнирное опирание, а две другие – свободны от опор?

22. Как определяются приведённые поперечные силы (контурные опорные реакции) в пластине с шарнирным опиранием по всем четырём сторонам?

23. Как определяются опорные реакции в углах пластины с шарнирным опиранием по контуру?

24. Сформулируйте правило знаков для приведённых поперечных сил и опорных реакций в углах пластины?

25. Какие существуют методы расчёта пластин?

26. Какие пластины допустимо рассчитывать в двойных тригонометрических рядах (методом Навье)?

27. Как записывается приближённое уравнение изогнутой поверхности пластины в виде двойного тригонометрического ряда?

28. Как раскладывается равномерно распределенная нагрузка в двойной тригонометрический ряд?

29. Из каких условий определяются коэффициенты ряда Фурье?

30. Как оценивается прочность пластины при изгибе?

31. Сформулируйте алгоритм расчёта пластины методом двойных тригонометрических рядов (методом Навье) с шарнирным опиранием по контуру.

Поиск по сайту: