Тема 3. Статистические распределения

Непрерывная СВ – СВ принимает любые значения.

Дискретная СВ – заданы ограничения.

Пр.1. 6 граней куба, если куб использовать в качестве игральной кости, - дискретные СВ.

Пр.2. При бросании «пера» возможны как дискретные, так и непрерывные СВ.

Распределение вероятностей – совокупность значений СВ и соответствующих им вероятностей. Его можно представить в виде таблицы.

Распределение разводов по годам семейной жизни

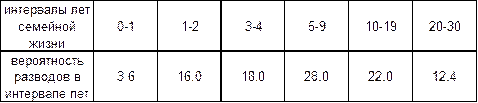Для непрерывной СВ вероятность появления ее точного значения всегда равна 0. Поэтому имеет смысл сравнивать размеры хотя бы малой площади Дх к размерам площади, соответствующей полной группе событий.

Плотность вероятности: f(x) = Дp/Дх – это вероятность, соответствующая единичному интервалу значений СВ,

где

Дp – вероятность попадания СВ х в интервал ее значений Дх.

Приблизим границы интервала Дх к точке х. Тогда и вероятность попадания в данный интервал станет меньше. При этом предел отношения Дp/Дх характеризует плотность вероятности, но уже в точке х:

.

В курсе математического анализа этот предел называется производной:

.

Распределение разводов по годам семейной жизни

Графическое представление распределения разводов по годам семейной жизни

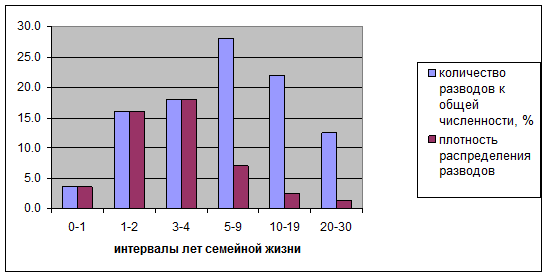Поэтому f(x) также называют дифференциальной функцией распределения вероятностей.

Для небольших интервалов Дх можно считать, что f(x) практически не меняется на этом интервале, и можно записать: Дp = f(x)Дх.

Рассмотрим пример с мишенью. Вероятность Дp численно равна площади заштрихованного столбика. Если ступеньки станут очень частыми, экспериментальная диаграмма перейдет в график идеальной функции плотности вероятности. Распределение, изображенное на рисунке, встречается очень часто и аналитически график этой функции записывается в виде:

.

Данная функция предложена в математике Гауссом, носит его имя и называется в теории вероятностей нормальным распределением.

Выясним основные характеристики полученного распределения:

Математическое ожидание -сумма произведений всех возможных значений случайной величины на их вероятности.

Мода - наиболее вероятное значение случайной вероятности, соответствующее максимуму плотности вероятности.

Медиана -значение признака, приходящегося на середину ранжированной (упорядоченной) совокупности.

Д исперсия -математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

С реднее квадратическое отклонение -квадратный корень из дисперсии.

А симметрия -отношение центрального момента третьего порядка к кубу среднего квадратического отклонения: .

Эксцесс -характеристика, которая определяется равенством: .

Положение и асимметрия