Пример 38.3

Найти минимум функции ,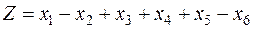

если

.

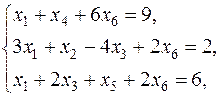
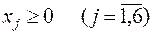Решение.

Запишем матрицу ограничений: .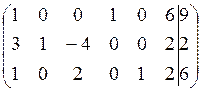

Единичные векторы 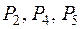принимаем за базис.

Свободным переменным присваиваем значения 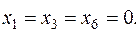Тогда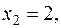

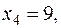
Следовательно, опорный план: .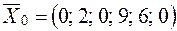

Значение целевой функции: .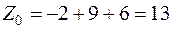

Проверим начальный опорный план на оптимальность. Для этого составим симплекс-таблицу (табл. 38.2).

Таблица 38.2

Симплекс- таблица (исходные данные – 1-я итерация)

Базис	Сбаз	сj		–1				–1
P0	P1	P2	P3	P4	P5	P6
P4 P2 P5	–1				–4
		–1	–1
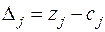
	–	–2

Последняя строка табл. 38.2 показывает, что начальный план не является оптимальным, так как имеем две положительные оценки: 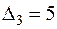, 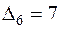. Поэтому переходим к новому опорному плану. Для этого вводим в базис вектор, для которого 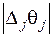наибольшее, где .

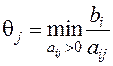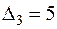: так как соответствующий столбец имеет один положительный элемент, то 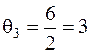. Тогда .

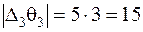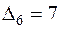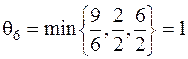: , тогда .

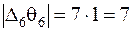Так как 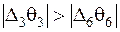, то в базис вводим вектор Р₃, разрешающий элемент 2 в последней строке.

Из базиса выводим вектор P₅, у которого единица в последней строке. Составляем новую таблицу (табл. 38.3). Пояснения к ее заполнению приведены ниже.

Таблица 38.3

Симплекс- таблица (2-я итерация)

Базис	Сбаз	сj		–1				–1
P0	P1	P2	P3	P4	P5	P6
P2 P4 ®P3	–1		½				½	6
	–2	–7/2	–1			–3/2
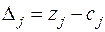
	–	–9/2				–5/2

Имеем новый базис: Р₂, Р₃, Р₄.

В столбце C_баз записаны коэффициенты при базисных неизвестных целевой функции: –1; 1; 1.

Заполняем строку вектора, который ввели в базис (Р₃). Для этого элементы третьей строки табл. 38.2 делим на разрешающий элемент 2. Получили разрешающую (ведущую) строку.

В столбце Р₃ необходимо получить единичный вектор. В первой строке табл. 38.2 имеем 0, поэтому эту строку перепишем без изменений. Во второй строке табл. 38.2 на месте элемента (–4) необходимо получить 0. Для этого каждый элемент ведущей строки табл. 38.3 умножим на 4 и прибавим к соответствующим элементам второй строки табл. 38.2.

Получим новый опорный план 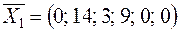. Проверим его на оптимальность. Для этого следует найти оценки векторов (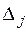). Есть одно положительное число 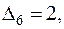план не оптимальный.

Переходим к новому опорному плану. Для этого вводим в базис вектор Р₆, так как только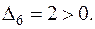

Находим отношение свободных членов к коэффициентам последнего столбца: , поэтому выводим из базиса вектор Р₄. Следовательно, разрешающим является столбец вектора Р₆ и строка вектора Р₄, а разрешающим элементом является 6.

Составляем новую таблицу (табл. 38.4).

Таблица 38.4

Симплекс- таблица (3-я итерация)

Базис	Сбаз	сj		–1				–1
P0	P1	P2	P3	P4	P5	P6
P2 ®P6 P3	–1 –1	3/2 3/2	1/6 1/3			–1 1/6 –1/6	1/2
	– 5	–23/6	–1		2/3	–3/2	–1
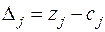
		–29/6			–1/3	–5/2

Имеем новый базис: Р₂, Р₃, Р₆. Заполняем строку вектора Р₆. Для этого элементы второй строки табл. 38.3 делим на разрешающий элемент 6 и записываем в табл. 38.4.

Получим ведущую строку. В столбце Р₆ надо получить единичный вектор. В первой строке табл. 38.3 требуется получить 0 на месте 1. Для этого каждый элемент ведущей строки табл. 38.4 надо умножить на (–6) и прибавить к соответствующим элементам первой строки табл. 38.3. Полученные элементы записываем в первую строку табл. 38.4.

В третьей строке табл. 38.3 на месте 1 нужно получить 0. Для этого каждый элемент второй строки табл. 38.4 нужно умножить на (–1) и прибавить к соответствующим элементам третьей строки табл. 38.3. Полученные элементы записываем в третью строку табл. 38.4. Получим новый опорный план: .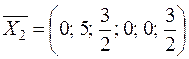

Проверим его на оптимальность. Для этого вычислим все значения и оценки векторов 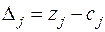. Все оценки 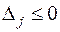. Следовательно, план 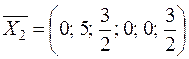оптимальный, так как свободные векторы Р₄, Р₅ имеют оценки .

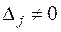Для полученного плана .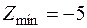

Поиск по сайту: