АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Исходные данные задачи о выпуске кирпича

Читайте также:
  1. Dan: 'данные о друзьях
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  4. I. Ситуационные задачи и тестовые задания.
  5. II. Основные задачи и функции
  6. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  7. II. Цель и задачи государственной политики в области развития инновационной системы
  8. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  9. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  10. Аналитические возможности, задачи и основные направления анализа СНС
  11. Аналитические данные к счету «Продажа продукции (работ, услуг)»
  12. Анатомо-физиологические данные.
Марка кирпича Вид глины Запас глины, т
     
     
     
Прибыль от реализации 1 тыс. шт. кирпича, грн     –
Количество выпускаемого кирпича, тыс. шт. –

 

Составим математическую модель задачи. Обозначим количество выпускаемого кирпича марки и – , тыс. шт. соответственно. Тогда прибыль от реализации всего кирпича , функция цели исследуется на максимум.

Составим систему ограничений: – количество глины , которое расходуется на изготовление всего кирпича, не превосходит имеющегося запаса. Рассуждая аналогично, получим ограничения по глине и :

Добавим условия неотрицательности .

Математическая модель задачи имеет вид:

 

,

.

Приведем систему ограничений к канонической форме. Для этого к левой части нерваенств системы добавим дополнительные переменные, тогда:

,

Решаем задачу с помощью симплекс-таблицы (табл. 38.6)

Таблица 38.6

Симплекс-таблица

№ п/п Базис           Примечания
                   
                , , – план не оптимальный, выполним симплекс-преобразование. , , , Так как , то в базис вводим вектор .
               
               
           
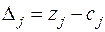
– –40 –70      

 

 

Продолжение табл. 38.6

                   
                [1]
            ½   [2]/2
            – 1   [2]·(–1)+[3]
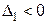            , , – план не оптимальный. , в базис вводим вектор .
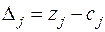
– –40        
                [4]
            ½   [5]
          –1 –1   [4]·(–1)+[6]
            , план оптимальный и единственный, так как для сво-бодных векторов . , .
–          

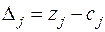
Так как в исходной задачи две переменные, то в ответе оставляем только , : ,

Подставим в систему ограничений:

 

Экономическая интерпретация результата: для того, чтобы получить максимальную прибыль в размере 1450 грн, требуется выпускать 10 тыс. шт. кирпича 1-й марки и 15 тыс. шт. кирпича 2-й марки, при этом глина первого и второго видов израсходована полностью, остался запас глины третьего вида.


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)