АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Арифметические действия над двоичными числами

Читайте также:
  1. I. ПРОБЛЕМЫ ВЗАИМОДЕЙСТВИЯ ПРИРОДЫ И ОБЩЕСТВА
  2. II. Пути противодействия психологическому воздействию противника.
  3. IV. Определите, какую задачу взаимодействия с практическим психологом поставил перед собой клиент.
  4. VI Обжалование решений, действий (бездействия) таможенных органов и их должностных лиц
  5. VI. Срок действия служебного контракта
  6. VII. По степени завершенности процесса воздействия на объекты защиты
  7. АВТОМАТИЧЕСКИЕ ВЕСОВЫЕ ДОЗАТОРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
  8. АВТОМАТИЧЕСКИЕ ВЕСОВЫЕ ДОЗАТОРЫ ПОРЦИОННОГО ДИСКРЕТНОГО ДЕЙСТВИЯ
  9. Аккультурация в межкультурных взаимодействиях
  10. Активность и степень воздействия на другие государственные орга-
  11. Активные действия
  12. Алгебраїчна форма запису комплексних чисел та дії над комплексними числами, записаними у цій формі
Сложение Вычитание Умножение
0 + 0 = 0 0 – 0 = 0 0  0 = 0
0 + 1 = 1 1 – 0 = 1 0  1 = 0
1 + 0 = 1 1 – 1 = 0 1  0 = 0
1 + 1 = 10 10 – 1 = 1 1  1 = 1

Правила арифметики во всех позиционных системах счисления аналогичны. В двоичной системе арифметическое сложение происходит так же, как в десятичной системе с учетом переноса единицы в старший разряд.

Пример 1. Выполнить операцию арифметического сложения (см. рисунок 1.1) в двоичной системе счисления. Точками показаны переносы.

 

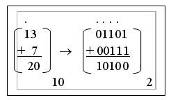
Рис. 1.1. Пример выполнения сложения в 10-ной и 2-ной системах счисления

 

Следует заметить, что в реальных ЭВМ чаще всего используются 16-, 32-, 64-разрядные сетки (машинные слова). Однако для учебных целей рассматривается простой вариант выполнения операции сложения.

Поскольку для построения цифровых устройств (ЭВМ) была выбрана двоичная система счисления, то основой для построения элементов компьютерной системы и для разработки алгоритмов программ является аппарат алгебры логики или булевой алгебры.

Логические функции «И», «ИЛИ», «НЕ» представляют собой функционально полную систему, с их помощью можно получить любое сложное высказывание из простых.

В сложных выражениях, сначала выполняется операция (отрицание «НЕ»), затем 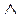(конъюнкция «И») и в последнюю очередь 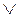(дизъюнкция «ИЛИ»). На основе этих логических функций и соответствующих электронных элементов выполняются более сложные функциональные узлы.

Отрицание можно представить с помощью следующей таблицы истинности (см. таблицу 4):

Таблица 4


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)