Структурные схемы алгоритмов

Структурные схемы представляют алгоритм в наглядной графической форме. Действия алгоритма помещаются внутрь блоков, соединенных стрелками, показывающими очередность выполнения действий алгоритма. Приняты определенные стандарты графических изображений функциональных блоков:

q действия ввода – вывода данных помещают в блоках, имеющих вид параллелограмма,

q действия обработки информации помещают в блоках, имеющих вид прямоугольников,

q команды проверки условий — в блоках, имеющих вид ромбов,

q начало и конец алгоритма обозначают овалом.

Структуры алгоритмов

Алгоритмы строятся из некоторых основных структур, состоящих из отдельных базовых элементов. Можно выделить три структуры (конструкции): линейная (последовательная), разветвляющаяся и циклическая.

Структура, состоящая из последовательности шагов (действий) называется линейной (см. рисунок 7.1). Каждый функциональный блок этой структуры имеет один вход и один выход.

Рис. 7.1. Линейная структура алгоритма

Структура, обеспечивающая выбор между двумя альтернативами в зависимости от исходных данных, называется разветвляющейся или условной. Различают полное (см. рисунок 7.2) и неполное (см. рисунок 7.3) ветвления. В этой структуре присутствует блок условия, который имеет один вход и два выхода (истина и ложь). После проверки условия на каждой ветви располагается линейная структура.

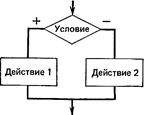
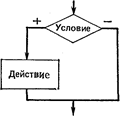
Рис. 7.2. Полная форма ветвления Рис. 7.3. Неполная форма ветвления

Структура, обеспечивающая повторение линейных и условных структур в зависимости от входных данных и условия задачи, называется циклической (или циклом). Различают циклы с предусловием (проверка условия стоит перед началом действий рисунок 7.4) и циклы с постусловием (проверка условия стоит после выполнения действий рисунок 7.5).

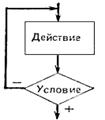
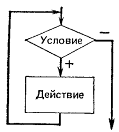
Рис. 7.4. Цикл с предусловием Рис. 7.5. Цикл с постусловием

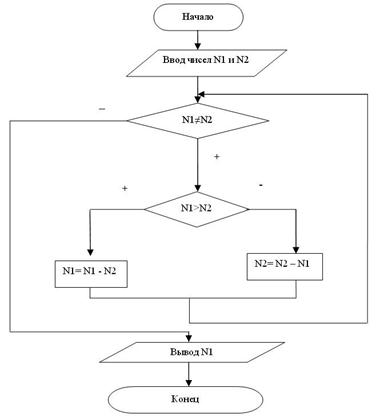Кроме перечисленных структур существуют подчиненные команды или процедуры, предназначенные для выполнения повторяющихся действий с разными входными данными. Пример структурной схемы приведен на рисунке 7.6.

Рис. 7.6. Пример структурной схемы алгоритма Евклида

Для записи внутри блоков действий используется естественный язык с элементами математической символики. В результате проверки условия возникают два возможных пути для продолжения алгоритма. Эти пути изображаются стрелками со знаками «+» и «-» (иногда пишут также «Да» и «Нет»).

Переход по стрелке со знаком «+» происходит, если условие истинно, а переход по стрелке «-», если условие ложно.

Схемы алгоритмов обладают большей наглядностью, чем словесная запись алгоритма. Однако эта наглядность быстро теряется при изображении большого алгоритма - в этом случае схема получается плохо обозримой.

При составлении алгоритмов следует учитывать начальные значения переменных, в которых будут накапливаться сумма или произведение, а также изменение переменной-индекса, т.е. порядкового номера значений последовательности чисел.

Задания:

Используя рассмотренные ранее структуры, создать следующие алгоритмы:

· Нахождение суммы последовательности чисел.

· Нахождение произведения последовательности чисел.

· Нахождение среднего значения последовательности чисел.

· Нахождение факториалов: n!, 2n!!, (2n+1)!! (раздельные алгоритмы и один – общий)

· Нахождение суммы всех положительных (отрицательных) чисел

· Нахождение максимального (минимального) значения последовательности чисел.

· Нахождение корней квадратного уравнения.

Поиск по сайту: