АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Построение кривых свободной поверхности

Читайте также:
  1. MathCad: построение, редактирование и форматирование графиков в декартовой системе координат.
  2. V. Построение одного тренировочного занятия
  3. Алгоритм цифровой подписи на основе эллиптических кривых ECDSA
  4. Анализ сопротивления до (прежде) содержания; анализ Эго до Ид; анализ, начиная с поверхности.
  5. Билет 12(Модель товарно-денежного кругооборота в условиях рынка свободной (чистой) конкуренции.)
  6. Борозды и извилины верхнебоковой поверхности полушарий
  7. Борозды и извилины медиальной поверхности
  8. Борозды и извилины нижней поверхности больших полушарий
  9. Вопрос 2. Построение доверительного интервала при неизвестном законе генерального распределения.
  10. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  11. Вычислите площадь поверхности цилиндра, если диаметр основания равен 12 см, высота 3,5 см.
  12. Движения мыщелков бедра по суставной поверхности большеберцовой кости во время осевой ротации

.

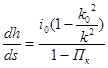i0<iк, h0>hкр.

РИСУНОК (лекции прошлый год)

- h>h0 и k>k0, => числитель > 0, и Пк<1 – знаменатель >0. => - функция возрастает – глубина возрастает вниз по течению – кривая подпора а1.

- h<h0 и h>hкр, k<k0, => числитель <0, и Пк<1 – знаменатель >0, => 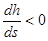- глубина потока уменьшается вниз по течению – выпуклая кривая спада b1.

- h<hкр, h<h0, k<k0, Пк>1 –числитель и знаменатель <0, => - глубина потока возрастает вниз по течению – вогнутая кривая подпора с1.

i0>iк. h0<hкр

РИСУНОК (лекции прошлый год)

- h>hкр, h>h0 и k>k0, Пк<1 – числитель и знаменатель <0, => 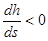- происходит подпор – кривая подпора а2.

- h>h0, h<hкр, k>k0, Пк>1 – числитель >0, знаменатель <0, => 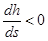- глубина уменьшается вниз по течению – кривая спада b2.

- h<h0, k<k0, Пк>1 – числитель и знаменатель <0, => - глубина потока возрастает вниз по течению – кривая подпора с2.

i0=iк,h0=hкр.

РИСУНОК(лекции прошлый год)

- h>h0 и k>k0, Пк<1 – числитель и знаменатель >0, => 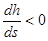- глубина возрастает вниз по течению - прямая а3.

- h<hкр, k<k0, Пк>1, => - кривая подпора, с3 –прямая.

 

2.Типы задач на неравномерное движение.

Первый тип: известны глубины h1 и h2, требуется определить расстояние l между этими сечениями. В зависимости от уклона дна потока l определяется по формулам:

При прямом уклоне: ,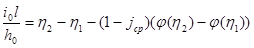

При нулевом уклоне: ,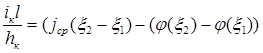

При обратном уклоне: . Для определяем , , , , , .

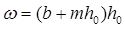Второй тип: известна глубина в одном из сечений (2-2), задано расстояние l между сечениями, необходимо определить глубину в сечении 1-1. решение методом последовательных приближений. Преобразуем: . Задаваясь произвольными h1, определяем левую часть уравнения. Далее задаваясь величиной η1, определяем φ(η1), подставляем в правую часть, пока уравнение не превратится в тождество. -> h1= η1h0 – первое приближение.

 

3.Определение длины кривой свободной поверхности потока при неравномерном движении по уравнению Бахметева.

Для русла с положительным уклоном дна: , где 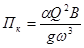. После преобразования: , где 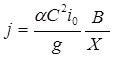. Выразим коэффициент Шези по формуле Маннинга, тогда: . Для широких и неглубоких русел В=Х, R=h. 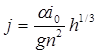. При этом дифференциальное уравнение примет вид: . После ряда последовательного разделения переменных и интегрирования, получим: .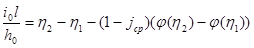

Для дна с горизонтальным руслом дна: равномерного движения не может быть, поэтому нормальная глубина отсутствует. После интегрирования получим: .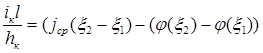

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)