Зонная пластинка. Попробуем разобраться, к каким эффектам приводит дифракция на круглом отверстии

Попробуем разобраться, к каким эффектам приводит дифракция на круглом отверстии. При этом не будем ни на минуту забывать, что спираль Френеля состоит из элементарных векторов, которые, соответственно, представляют колебания от элементарных колечек круглого фронта падающей волны. Вся спираль представляет колебания от полностью открытого фронта (k ® ¥), если открыта часть зон Френеля, “реализуется” лишь часть спирали. Амплитуда суммарных колебаний представляется длиной вектора, соединяющего начало спирали и ее конец.

0,5 1 1,5 2 2,5 E0

Проиллюстрируем эти слова. На рисунке показаны случаи, когда открыта половина первой зоны, первая зона, полторы зона, две и две с половиной. Иначе говоря, когда радиус круглого отверстия равен радиусу половине первой зоны Френеля, радиусу первой зоны и т.д.

1 2 3 4 5 ...   ; ; ;

Витки спирали для первых зон Френеля им будем считать окружностями. Поэтому на рисунке выписаны такие значения амплитуды суммарных колебаний E. Подсчет амплитуд колебаний производится приближенно, но для нас важно понимание причин изменения амплитуд при изменении радиуса отверстия, хотя бы и за счет некоторого снижения точности.

При суммировании амплитуд колебаний от первой, второй и т.д. зон Френеля мы должны получить амплитуду E₀. Но если бы мы складывали только колебания от четных или только от нечетных зон Френеля, мы получили бы колебания с амплитудой, модуль которой намного превосходит величину E₀. Действительно, вместо суммы членов знакопеременного ряда мы бы тогда складывали значения E одного знака.

Технически такое сложение осуществляется с помощью зонной пластинки. Она представляет собой систему непрозрачных концентрических колец, которые закрывают, например, нечетные зоны Френеля. Амплитуда колебаний в точке наблюдения при использовании такой пластинки сильно возрастает.

Зонная пластинка действует в этом случае подобно линзе, которая фокусирует свет в некоторой точке. Соответственно, для зонной пластинки может быть введено фокусное расстояние. На рисунке показана зонная пластинка, закрывающая нечетные зоны Френеля. Разность хода нарисованных лучей равна l, и амплитуда колебаний от открытых зон при одинаковых знаках складываются по модулю. Поэтому и получается большая интенсивность колебаний в точке наблюдения, фокусировка лучей.

Следующим шагом в своего рода совершенствовании зонной пластинки является превращение ее в прозрачную фазовую зонную пластинку. Вместо того, чтобы закрывать, например, нечетные зоны Френеля, мы можем изменять на p фазу приходящих от них колебаний. Тогда амплитуда колебаний в точке наблюдения примерно удвоится. Чтобы достигнуть этого, необходимо изменить для них оптическую длину пут на половину длинны волны, обеспечить выполнение условия , где d - толщина фазовой пластины из материала с показателем преломления n.

7. Дифракция плоских волн на щели.

Поскольку решетка состоит из щелей, рассмотрим формирование дифракционной картины на одной из них. При наблюдении дифракции Фраунгофера источник и экран «находятся на бесконечно больших расстояниях» от щели (дифракционной решетки или другого препятствия), т.е. на щель падает волна с плоским волновым фронтом, и после прохождения щели мы анализируем интерференцию волн от вторичных источников в бесконечно удаленной точке. Если - расстояние до источника, - расстояние до экрана, - длина волны света, - ширина щели, то должно выполняться соотношение (1). Экспериментально световая волна формируется лазером (при необходимости пучок расширяют) или точечным источником, расположенным в фокусе собирающей линзы. За щелью располагают экран на большом расстоянии от нее или сразу за щелью располагают собирающую линзу, в фокальной плоскости которой наблюдают дифракционную картину на экране. Возможны и другие способы размещения источника и экрана, для которых не выполняется соотношение (1), но они выходят за рамки данной лекции.

Удобно анализ дифракционной картины проводить при помощи комплексных чисел. Разобьем вспомогательную поверхность на элементы одинаковой площади 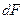. Тогда каждый из вторичных источников вносит одинаковый по модулю вклад в амплитуду результирующего сигнала в точке наблюдения: . В соответствии с графическим представлением комплексных чисел можно представить в виде «стрелки» на комплексной плоскости.

Поиск по сайту: