Напомним, что

каждому комплексному числу 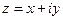на плоскости с прямоугольной системой координат можно сопоставить точку с координатами (и соответственно радиус вектор, проведенный в эту точку). Числа и называют вещественной и мнимой частями числа . В полярной системе координат длина радиус вектора 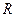называется модулем комплексного числа , а угол поворота радиуса вектора называется аргументом. Выполняются соотношения, связывающие алгебраическую, тригонометрическую и показательную формы записи комплексных чисел:

, и соответственно , . Подробнее смотрите, например [2].

Рисунок 1 — Представление комплексных чисел в прямоугольной системе координат.

В рассматриваемом случае дифракции на решетке, вклад от каждой из ее щелей мал и составляет 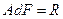. С учетом сдвига фаз он может быть представлен алгебраически в виде – действительной части комплексного числа или геометрически в виде проекции радиус вектора комплексного числа на горизонтальную ось. Соответствующая сумма вкладов от щелей решетки может быть представлена как , что соответствует проекции вектора суммы комплексных чисел на горизонтальную ось .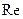

В рассматриваемом случае каждая щель в соответствии с принципом Гюйгенса-Френеля создает вторичную волну. Интенсивность излучения света в точке наблюдения дифракционной картины обусловлена интерференцией вторичных волн и определяется в результате сложения соответствующих векторов. Сигнал от каждой из щелей дифракционной решетки определяется своим вектором на комплексной плоскости и соответствующим ему комплексным числом 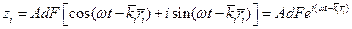, тогда результат интерференции волн можно представить в виде вектора. Производя суммирование, получаем: . Длина вектора, соответствующего числу , будет определяться модулем каждого из комплексных чисел и слагаемым 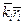. Поскольку мы разбили площадь вспомогательной поверхности внутри щели на одинаковые участки 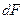, то модули всех одинаковы. Множитель обуславливает вращение каждого из векторов, а значит суммарный вектор будет вращаться с постоянной угловой скоростью 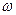против часовой стрелки.

Рисунок 2 — Оптическая схема установки для наблюдения дифракции Фраунгофера на щели. И – источник излучения, К – конденсор (линза, фокусирующая излучение на щель), Щ – освещенная щель, играющая роль точечного источника, (располагается в фокусе линзы), Л₁ – линза, формирующая плоскую волну, О – объект, на котором происходит дифракция (щель), Л₂ – линза, фокусирующая излучение на экран, Э – экран (располагается в фокальной плоскости линзы).

8. Рисунок 3 — Дифракция Фраунгофера на щели.

Рассмотрим дифракцию на щели. Разобьем фронт плоской световой волны, прошедшей через щель, на полосок одинаковой ширины – вторичные источники света. Тогда вклад от каждого из них будет одинаков по модулю, а сдвиг фаз между соседними вторичными источниками, будет определяться шириной полоски и углом между нормалью.

Выберем две точки и волнового фронта волны, падающей на щель. Тогда для анализа интенсивности плоской световой волны, распространяющейся после дифракции на щели под углом относительно нормали к плоскости объекта, разность фаз между ними будет равна (треугольник ABC – прямоугольный). Таким образом, если всю щель равномерно разбить на участки одинаковой площади, то вектора будут иметь одинаковую длину, а сдвиг фаз между каждыми двумя последовательными векторами будет составлять , где - ширина щели, - число участков, - суммарный сдвиг фаз между первым и последним векторами (соответствуют краям щели). Получаем фигуру, которая в пределе переходит в дугу окружности [3].

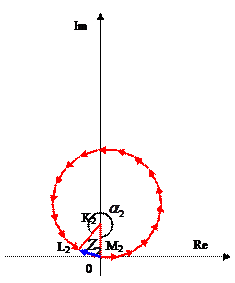
Рисунок 4 — Векторные диаграммы для расчета интенсивности картины дифракции
Фраунгофера на щели.

9.

На рисунках для случая представлены векторные интерпретации образования векторов суммы 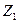и для двух суммарных сдвигов фаз и , соответствующих различным точкам наблюдения на экране. Из геометрических соображений находим радиусы окружностей , и значение модуля вектора суммы . Поскольку все вектора «вращаются» с одинаковой угловой скоростью 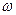, то наибольшая интенсивность в каждой точке наблюдения будет определяться модулем вектора суммы. Интенсивность света может быть вычислена по формуле:

, где 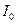- интенсивность света в точке, в которой сдвиг фаз равен нулю. При падении света по нормали сдвиг фаз равен нулю при распространении света по нормали при . Если излучение на объект (щель) падает под углом относительно нормали, то сдвиг фаз будет определяться формулой 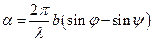. Нулевой сдвиг фаз будет в направлении свободного распространения света 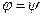, как если бы дифракции на объекте (щели) не было. Графики, соответствующие зависимостям и от сдвига фаз , построены сине-зеленым и синим цветами соответственно.

Рисунок 5 — Зависимость интенсивности от сдвига фаз (от угла дифракции) для дифракции Фраунгофера на щели (синий график).

Точки минимума интенсивности определяются из равенства 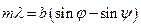, . Большая часть энергии сосредоточена в диапазоне углов .

Поиск по сайту: