Зоны Френеля. При знакомстве с дифракцией в параллельных лучах (при бесконечных расстояниях до источника света и до зоны наблюдения) их параллельность сильно упрощала

При знакомстве с дифракцией в параллельных лучах (при бесконечных расстояниях до источника света и до зоны наблюдения) их параллельность сильно упрощала математические проблемы необходимых расчетов, хотя результаты и их смысл не становились от этого очень простыми. Теперь нам придется иметь дело со сферическими волнами, их лучи, разумеется, не параллельны друг другу. Это усложняет нужную для расчета математику, большинство задач поэтому мы будем решать приближенно. Но вначале оставим хотя бы расстояние до источника бесконечным - рассмотрим дифракцию плоской волны на круглом отверстии.

Ds P P

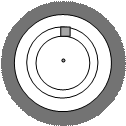
В соответствии с принципом Гюйгенса-Френеля каждый элементарный участок фронта Ds может быть рассмотрен как точечный источник сферических волн. Такой участок показан на рисунке. Точка наблюдения p в наших задачах, как правило, будет находиться на оси симметрии на некотором расстоянии от отверстия или от круглой преграды. Разумеется, от различных элементарных участков фронта свет к точке наблюдения будет проходить разные расстояния и при сложении колебаний нам необходимо будет учитывать разности фаз dj отдельных колебаний. Но разности фаз dj, понятно, будут нулевыми, если элементарные участки расположены в пределах тонкого кольца, и тогда (пока мы не перешли к другому кольцу) мы можем просто складывать амплитуды колебаний волн, приходящих от таких участков. Поэтому и сами элементарные участки мы будем выбирать в виде тонких колец. Фаза колебаний в точке наблюдения будет зависеть от радиуса такого кольца.

Итак, рассмотрим падение плоской волны на круглое отверстие и проанализируем, как зависит от радиуса отверстия амплитуда суммарных колебаний в точке наблюдения.

L r q=r/b q/2 b P

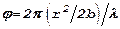
Из рисунка видно, что разность хода лучей от края кольца радиуса r и от центра отверстия

.

Поэтому от кольца с радиусом r колебания будут приходить с запаздыванием по фазе на

.

С помощью векторной диаграммы мы будем складывать колебания, приходящие в точку наблюдения от тонких колечек толщиной Dr. Соответствующие векторы на фазовой диаграмме будут повернуты по отношению друг к другу на угол

j=p Dj

.

При достаточно большом радиусе будет

.

Соответствующий радиус r₁ называется (внешним) радиусом первой зоны Френеля. При дальнейшем увеличении радиуса, естественно, величина j будет увеличиваться. Из условия j=kp мы получаем выражение для радиуса k -й зоны Френеля:

; .

E0

Мы уже достаточно много работали с векторными диаграммами, и должно быть понятно, что при дальнейшем увеличении радиуса отверстия (по сравнению с r₁) амплитуда суммарных колебаний в точке наблюдения, пропорциональная длине отрезка (вектора), соединяющего начало и конец дуги, будет уменьшаться. Она достигнет минимума, когда радиус отверстия достигнет внешнего радиуса второй зоны Френеля. Но в отличии от задачи о колебаниях волны, излучаемой щелью при дифракции Фраунгофера, дуга не замкнется в окружность, мы получим некоторую скручивающуюся спираль. Длина вектора, проведенного от начала к центру спирали, дает, очевидно, амплитуду падающей волны - скручивание спирали к центру соответствует бесконечно большому радиуса отверстия, когда дифракция не наблюдается.

Подобная спираль, которую называют спиралью Френеля, получается и в том случае, когда на отверстие падает сферическая волна конечного радиуса a. Выражение для радиусов зон Френеля в этом случае, естественно, иное.

a 1 | 2 | 3 | 4 | 5 | Поиск по сайту: