 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Если отверст. открыв. четное число зон Френеля то в т. P наблюд. min, если нечетное – то max
Пусть на пути сферич. фронта свет. волны распол. круглый непрозрачный диск, к-й закрыв. 1-е m зон Френеля.
A= Am+1-Am+2+Am+3-Am+4+…=Am+1/2+(Am+1/2-Am+2+ Am+3/2)+(Am+3/2-…=Am+1/2
Видно что в т.P всегда наблюд. max. Расчитаем радиус зон Френеля.
rm2=a2-(a-h)2=(b-ml/2)2-(b+h)2, пренебрегая величинами порядка l2 окончательно получаем
rm=Ö(abml/(a+b) сферический фронт свет. волны
rm=lima®¥Ö(abml/(a+b))=Ö(bml) -плоский фронт свет. волны.
2. Уравнение Шредингера для квантового гармонического осциллятора и его решение. Энергия квантового гармонического осциллятора. Нулевые колебания.
Гармонический осциллятор - частица, на которую действует сила стремящаяся вернуть её в положение равновесия и пропорциональная величине смещения частицы из положения равновесия. F=-Ux; U=1/2*k*x(c.2); w=√k/m`; k=mw(c.2);
U=1/2*mw(c.2)x(c.2), где w-частота собственных колебаний частицы. Уравнение Шредингера для гармонического осциллятора (ГО) будет:
d(c.2)Ψ/dx(c.2)+(2m/ħ(c.2))*(E-(mw(c.2)x(c.2)/2))*Ψ=0. Это уравнение имеет решение при собственных значениях энергии: En=(n+(1/2))ħw, n=0,1,2,… Видно, что энергия ГО квантуется. Нулевые колебания. Согласно классической физике при абсолютном нуле температуры всякое движение прекращается. Рассмотрим энергию квантового ГО. При уменьшении температуры n будет уменьшатся и при абсолютном нуле n станет =0. Однако, E0=ħw/2, т.е. энергия не равна 0. Эта энергия наз-ся энергией нулевых колебаний, а сами колебания- нулевыми, т.е. согласно квантовой механике при абсолютном нуле температуры движение не прекращается: остаются нулевые колебания.
3. Взаимопревращение нуклонов при β-распаде.
Бета - распад объединяет три вида ядерных превращений электронный (β-) распад, позитронный (β+} распад и электронный захват. При изучении В - распада пришлось столкнуться со следующими фактами: I. В отличие от α - распада, где α - частица имеет определенное значение энергии, при β - распаде кинетические энергии вылетающих электронов (позитронов) лежат в пределах от 0 до Емакс, т.е. вылетающие электроны имеют сплошной спектр. Величина Емакс=(my+me-mx)c2 имеет, определенное значение для каждого изотопа Сплошной β - спектр как бы - противоречит закону сохранения энергии, т.к. нет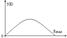 
определенной энергии Е β, у вылетающей частицы 2. После открытия нейтрона стало ясно, что ядра атомов состоят из протонов и нейтронов и в их состав не входят ни электроны, ни позитроны. 3. Электрон или позитрон, вылетающие приβ - распаде уносят с собой собственный момент количества движения.(спин), равный ħ/2 => ядра с четным числом нуклонов, обладающие целым спиной, после β -распада должны были бы иметь полуцелый спин при четном числе нуклонов.
Для преодоления указанных трудностей Паули предложил гипотезу нейтрино. Согласно этой гипотезе в каждом акте β - распада наряду с β - частицей испускается еще другая незаряженная частица со спином ħ /2 При позитронном распаде испускается нейтрино (AZX-> AZ-1Y+ 0-1e- v), а при электронном – антинейтрино (AZX-> AZ+1Y+ 0-1e+ v~). Они отличаются направлением спина. В третьем типе β - распада - электронном захвате материнское ядро с избытком протонов захватывает орбитальный электрон из атомных оболочек. После захвата, как и в позитронном распаде, один протон превращается в нейтрон: 
. Электронный захват обозначают как и оболочку К-захват, L- захват и т.д.
Билет №16
1. Вращение плоскости поляризации.
Некоторые вещества, называемые оптически активными обладают способностью, при пропускании через них линейно поляризованного света, поворачивать плоскость поляризации. К ним относятся кварц, растворы оптически активных веществ (раствор сахара и др.). Кристаллические вещества сильнее всего вращают плоскость поляризации, если свет распространяется вдоль оптической оси, Угол поворота φ пропорционален пути луча l в кристалле φ=αl
Здесь φ- постоянная вращения. Например, для кварца α=21,7 град/мм. В растворах угол поворота φ зависит и от концентрации активного вещества: φ=[α]cl
Здесь [α] - величина, называемая удельной постоянной вращения. Различают право и левовращающие вещества.
Это явление вызывается особым расположением ионов кристалла вокруг рассматриваемого направления.
2. Распределение энергии по длинам волн в спектре излучения абсолютно черного тела. Законы Вина.
Аб. ч. тело–это тело к–е полностью поглощ. падающий на него излучение (не отраж.). Моделью а.ч. тела может служить маленькое отверстие в полой сфере.
Анализ получ. эксперимент. закономерн. позволили сформул. законы излуч.
1) Стефана–Больцмана Rэ=sT4, пост. Ст–Б. s=5.71*10–8, если тело не яв–ся А.ч. то Rэ=ksT4, где k–нек–ий коэф. наз. степенью нечерноты 0<=k<=1
2) Закон смещения Вина lmax=b/T, b–1–я пост. Вина b=2.898*10–3, lmax–длина волны на к–ю приход. max излучательной способн. А.ч.тела.
3) 2–й закон Вина e0(lmax,T)=b1T5, b1–2–я пост. Вина b=1.29*10–5,
Попытки дать объясн. эксперим. кривой e(l,T) на основе класич физики приводили к завис.: e(l,T)~1/l (Рэлея–Джинса).
Формула Р.–Д. согласовывается с экспериментальной кривой только в области больших длин волн при l®0 => e(l,T)®¥.
Расхождение ф. Р.–Д. с экспериментальной кривой в области малых длин волн было названо “ультрафиолетовой катастрофой”. Классич. физика оказалась не способна объяснить излучен. нагрет. тел. Получить теорет. зависимость e(l,T) удалось Максу Планку путем отказа от теории о непрер. излучен. энергии нагрет. тел.
3. Закон радиоактивного распада. Период полураспада и время жизни радиоактивного ядра. Активность радиоактивного изотопа.
Отдельные радиоактивные ядра испытывают распад независимо друг от друга, поэтому количество распавшихся ядер dN за время dt пропорционально числу имеющихся ядер N и времени-(1),где λ- постоянная распада, характерная величина для данного вещества. Знак минус указываот на убыль радиоактивных ядер. Из (1) находим уравнение (закон) радиоактивного распада, где N0- начальное количество ядер, N - количество нераспавщихся ядер к моменту времени t. 
Время, за которое распадается половина первоначального количества ядер, называется периодом полураспада Т _.
Т.к. активность распада ядра носит случайный характер, то постоянная распада λ характеризует.вероятность распада. Обратная же ей величина называется средним временем жизни радиоактивного ядра: 
Радиоактивные вещества характеризуются активностью, равную числу ядер, распадающиеся за 1 с: 
За единицу активности принят 1Бк (беккерелях) = 1распад/с. Часто пользуются внесистемной единицей I Кю (кюри) равно3,7*1010 расп/с. Активность радиоактивного вещества массой m равна 
где NA – число Авогадро, А – атомная масса.
Билет №17
1. Поглощение света. Закон Ламберта-Бера. Причина поглощения света в диэлектриках и проводниках.
Поглощение света или адсорбция – это уменьшение интенсивности света при распрост. волны в вещ. (фронт волны плоск.). При поглащ. энергия эл-маг. волны переходит во внутр. энергию поглощающ. вещ-ва (оно нагревается). Рассм. слой погл. вещ-ва толщ. l, пусть на него падает параллель. пучек света интенс. I0 вылим внутри поглощ. слоя слой dx. Уменьшение интенс. света при прохождении слоя толщины dx: dI~–Idx, dI=–aIdx. Интегрируя получаем закон Ламберта–Бугера: I= I0e–al, I–интенс. света прошед. слой поглощ. вещ–ва толщ. l. Если поглощ. вещ–во растворено в непоглощ. раствор. то a0=a1c, где c–концентр. поглощ. вещ–ва, a1–коэф. поглощ. отнесен. к ед. конц. a1,a зависят как от природы поглощающегося вещ–ва так и от длины волны падающ. света.
Диэлектрики, в них нет своб. эл–в, поглощ. света обусловл. по резон. при вынуж. колеб. эл–в в атомах, поэтому поглащ. света селективно.
Металлы–в них много своб. эл–в, в поле падающ. свет. волн своб. эл–ны соверш–ют след. движен. и получ. вторич. волны. Накопление первич. и вторрич. волн дает интенсивно отраженную волну слабо преломленную, быстро затух. ее энергия перех. в тепло. Поглощ. света в металле не селективно. Т.к. аномальная диспер. света наблюд. на част–х близких к част–м собств. колеб. эл–в в атомах на к–х вещ–во сильно поглощ. свет, то аномальная диспер. наблюд. в области полос поглощ. вещ–ва.
2. Физическая природа химической связи. Обменное взаимодействие.
Для объяснения образования отдельных молекул химия вынуждена была ввести понятие о некот-х химич-х силах. Однако позже установили: никаких хим. сил нет и все они сводятся к обычным электрическим взаимодействиям заряженных частиц. Различают 2 вида связей м\у атомами в молекуле: гетерополярная(ионная) и гомеополярная (ковалентная). При гетерополярной связи электроны от одного атома переходят к другому и связь возникает за счёт разноименно заряженных частиц. Ковалентные связи обусловлены тем, что при образовании такой связи электроны отдельных атомов обобществляются. Ковалентная связь имеет квантово-обменный характер. Обменное взаимодействие - специальное взаимодействие тождественных частиц. Оно эффективно возникает в том случае, если перекрываются волновые функции отдельных частиц.
3. Собственные и примесные полупроводники и их зонная структура. Положение уровня Ферми в них.
Полупр-ки – в-ва, у к-х ширина запрещ-й зоны составляет величину порядка 1 эВ.
Рассм полупров-к, в к-м часть атомов основного полупр-ка заменена атомами в-ва валентность, к-х отлич-ся валентностью основного полупр-ка.
Пусть в 4х валент. Полупр-к внедрены атомы 5валент примеси.
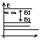В случае 5валент примеси 4 эл-на этой примеси будут задействованы в образ-и межатомных связей в кристалле.
5й эл-н примеси в создании связи не участвуют, и поэтому оказ-ся слабосвяз-м в атомной примеси.
При увел-и темп-ры полупр-ка отрыв-ся прежде всего этот 5й эл-н, при этом обр-ся своб эл-ны, но дырки при этом не образ-ся.
Такая примесь наз-ся донорной примесью.
В случае донорной примеси проводимость полупроводника яв-ся электронной, а сам полупр-к наз-ся полупр-к n-типа.
В случае донорной примеси энерг уровни нах-ся у потолка запрещ зоны. Уровень Ферми в полупр-ке n-типа смещен по напр-ю к потолку запрещ зоны.
Рассм-м 4х валентный полупр-к в к-й внедрена 3х вал-я примесь.
В этом случае одна из связей оказ-ся недоукомплектованной эл-ном. Эту связь может доукомплектовать эл-н из соседней связи основного полупр-ка. При этом своб-е эл-не не появ-ся.
Такая примесь наз-ся акцепторной. А сам полупр-к – полупр-ком p-типа. В полупр-ке p-типа проводимость дырочная. В случае акцепторной примеси энерг уровни нах-ся у дна запрещ зоны.
Хим-ски чистые в-ва яв-ся собств полупр-ками. Рассм 4хвалентный полупр-к Ge (германий). Четыре связи с соседними атомами, образованы восемью эл-нами (по четыре от каждого атома). Каждый эл-н обр-ет связь с противоположно направ-ми спинами. При низк темп-ре все связи оказываются укомплектованными эл-нами и своб эл-нов в полупр-ке нет. При увел темп-ры за счет энергии хим-го дв-я происходит отрыв эл-нов от одной из связи. При этом на месте ушедшего эл-на остается дырка. Дырка локализована на какой-то одной связи в кристалле и своб перем-ся по кристаллу не может. Оторвавшийся же эл-н может своб-но перем-ся по кр-лу.
Если приложить внешнее эл поле, то эл-н будет перем-ся против поля. Дырку же может занять эл-н из соседней связи. Путем таких перескоков дырка будет перем-ся по полю, а эл-н против поля. Дв-е дырки можно рассм-ть как дв-е полож заряж частиц. Когда своб эл-н занимает место дырки исчезает одновременно и своб эл-н и дырка. Такой процесс наз-ся рекомбинацией. Т о в хим-ски чистых полупр-ках появл-ся одновр-но своб эл-ны и дырка, причем кол-во их одинаково. Проводимость собств полупр-ков яв-ся электронно-дырочными. С т з зонной теории эл-н задействованный в создании хим-х связей в кр-ле нах-ся в валентной зоне.
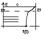
При сообщении ему достаточной энергии он преодолевает запрещ-ю зону и переходит в зону проводимости. При этом в валентной зоне образ-ся дырка. Такой переход будет осуществляться прежде всего с верхних уровней валентной зоны. По мере увеличения энергии в зону проводимости будут переходить эл-ны со все более глуб-х уровней валентной зоны. Поэтому энергия дырки тем больше, чем глубже она нах-ся в валентной зоне. Эл-н в зоне проводимост и дырку в валентной зоне можно рассм-ть как своб-е носители заряда в собств полупр-ке. По мере увел-я темп-ры число таких носителей будет возрастать. Уровень Ферми в собств полупр-ках нах-ся в сер-не запр-й зоны.
Билет №18
1. Дифракция Френеля на круглом отверстии и круглом непрозрачном диске. Используя метод зон Френеля, получите выражение для амплитуды результирующего колебания световой волны для этих случаев.
Френель предложил объединил симметрич. т-ки световой волны в зоны выбирая конфигурацию и размеры зоны такие что разность хода лучей от краев 2-х соседних зон от т-ки наблюдений была бы равна l/2 и след-но от краев 2-х сосдних волн приход. в т-ку наблюдения в противофазе и при наложении др. на др. ослабивают.
Обозначим ч/з A1 амплитуду кол-й в т-ки P даваемым всеми т-ми источниками нах. внутри 1-й зоны Френеля. Ясно что A1 > A2 > A3…
Результат амплитуды кол-й в т.P даваемое всеми зонами Френеля будет A = A1 - A2+A3 - A4…, A=A1/2+(A1/2-A2+ A3/2)+(A3/2-A4+ A5/2)+…=> A=A1/2. Видно что в том случае, если открыты все зоны Френеля то амплитуда кол-й = половине амплитуды кол-й даваемой 1-й зоной Френеля.
Пусть на пути сферич. фронта свет. волны распол. непрозрачный экран, к-й открыв. 1-е m зон Френеля.
1. четное A=A1/2+(A1/2-A2+ A3/2)+ A3/2+…+ (Am-1/2-Am)=A1/2+Am-1/2-Am=(A1+Am-1)/2-Am
2. m-нечетное A=A1/2+(A1/2-A2+ A3/2)+…+ (Am/2-Am-1 Am/2)+Am/2=A1/2+Am-1/2-Am=(A1+Am-1)/2-Am, => A=(A1+Am)/2
Поиск по сайту: