Дифракция Френеля в сходящих лучах

В этом случае на препятствие падает сферическая волна, а экран находится на конечном расстоянии от него. При дифракции Френеля на экране, находящемся на конечном расстоянии от препятствия, получается «дифракционный образ» препятствия.

9.3. Дифракция Фраунгофера на щели

Пучок параллельных волн исходит от источника, расположенного далеко от препятствия. Если источник расположить в фокусе собирающей линзы, тогда после прохождения линзы пучок волн будет параллельным.

Установка для наблюдения дифракции Фраунгофера на щели состоит из непрозрачного экрана E, в котором вырезано длинное узкое отверстие, собирающей линзы Л и экрана Э, на котором наблюдается дифракционная картина (рис. 9.5).

Параллельный пучок монохроматического света падает на экран Е и проходит через отверстие. Плоскость щели совпадает с фронтом падающей волны, поэтому все точки щели являются вторичными источниками, они колеблются в одинаковой фазе. Волны, идущие параллельно главной оптической оси линзы, имеют одинаковую оптическую длину пути, поэтому на экране Э в центре дифракционной картины будет видна светлая полоса (центральный максимум нулевого порядка, m = 0). Волны, идущие вдоль побочной оптической оси, имеют оптическую разность хода, которая зависит от угла наблюдения j.

Найдем условия наблюдения максимума и минимума при дифракции Фраунгофера. Разделим плоскость щели шириной b на зоны, параллельные краям щели так, чтобы оптическая разность хода соседних волн от краев щели составила . Найдем оптическую разность хода волн D =ВС, идущих от краев щели. Опустим с этой целью перпендикуляр АС и находим D = b sinj.

Рис. 9.5.

При четном числе зон Френеля на длине D укладывается четное число полуволн:

D = 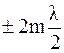, (m =1, 2,...),

тогда волны от двух соседних зон приходят в точку F_j на экране Э в противофазе, поэтому взаимно компенсируют друг друга и наблюдается дифракционный минимум.

В случае нечетного числа зон Френеля:

, (m =1, 2, …),

волна от одной зоны остается нескомпенсированной и наблюдается дифракционный максимум. На рис. 9.6 представлен график зависимости интенсивности света от sinj.

Рис. 9.6.

Минимум интенсивности возникает при условии:

sin j = , (m =1, 2, …).

Дифракционная картина симметрична относительно центра линзы Л:

.

Число наблюдаемых минимумов найдем из условия:

.

Учитывая условие минимума, запишем:

,

отсюда число минимумов:

. (9.4)

Найдем угловую ширину центрального максимума нулевого порядка. Краям центрального максимума соответствует условия:

,

откуда:

= , (9.5)

при условии , .

9.4. Дифракционная решетка

Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние, щелей шириной b, разделенных непрозрачными промежутками шириной а (рис. 9.7).

Величина d = a + b называется периодом дифракционной решетки. Для видимого света дифракционной решеткой может служить прозрачная стеклянная пластинка с рядом тонких параллельных штрихов, нанесенных на нее алмазом.

Пусть плоская монохроматическая волна падает нормально на решетку. Каждая из щелей решетки дает на экране дифракционную картинку. Линза собирает волны от всех щелей, идущие под углом j. Амплитуды колебаний, создаваемых каждой щелью в точке О будут одинаковы.

В центре экрана амплитуда A = NА₀, где N – число щелей. А₀ – амплитуда колебаний от одной щели.

Результирующая амплитуда колебаний возрастает в N раз, а интенсивность - в N² раз, так как волны, идущие от всех щелей при j = 0 сходятся в точке О без дополнительной разности хода (свойство собирающей линзы). Оптическая разность хода волн, идущих вдоль главной оптической оси, равна нулю.

Рис. 9.7.

Волны, идущие от разных щелей под углом j, сходятся в точке Р, проходят различные пути и имеют разность фаз d.

Колебания от всех щелей можно считать когерентными. Согласно результату, полученному при расчете многолучевой интерференции:

, (9.6)

где I_j – интенсивность создаваемая одной щелью.

Заметим, что в случае некогерентных колебаний результирующая картина от N щелей давала бы интенсивность:

.

Поскольку оптическая разность хода от соседних щелей , то разность фаз

, (9.7)

где l - длина волны в данной среде.

Подставив в (9.6) выражение для интенсивности света, создаваемой одной щелью I_j и разность фаз (9.7), получим:

, (9.8)

где I₀ – интенсивность колебаний в точке М, соответствующая углу j = 0.

1. Интенсивность света от каждой щели в отдельности обращается в ноль при условии:

, , (9.9)

где - порядок минимума.

Отсюда следует .

2. Максимум интенсивности света достигается при условии:

, 0, 1, 2…, (9.10)

где к – порядок главных максимумов.

С увеличением числа щелей дифракционной решетки увеличивается интенсивность главных максимумов и уменьшается их ширина, следовательно, возрастает четкость дифракционной картины.

График функции для N = 4, , представлен на рис 9.8.

Главные максимумы 3, 6, и т.д. порядка пропадают, так как они приходятся на минимумы интенсивности от одной щели.

Дифракционная решетка применяется для спектрального анализа излучения. Пусть дифракционный максимум порядка наблюдается под углом , тогда из условия:

можно определить длину волны излучения:

. (9.11)

Рис. 9.8.

Максимальное число наблюдаемых дифракционных спектров определяется из условия:

.

Находим:

, (9.12)

поскольку .

Угловая ширина максимума k-того порядка:

. (9.13)

Угловая дисперсия решетки:

. (9.11)

Пусть на решетку падает немонохроматический свет. Для каждой длины волны условие максимума выполняется при различных углах j. поэтому дифракционная картина представляет собой ряд цветных полос, т.е. дифракционный спектр. Получение и анализ спектров имеет большое значение в оптике. Изучение спектров испускания и поглощения позволяет установить энергетические уровни атомов.

9.5. Дифракция Френеля на круглом отверстии

Рассмотрим дифракцию волн от источника, расположенного близко от препятствия.

На пути сферической волны от близко расположенного источника, поставим экран с вырезанным в нем круглым отверстием радиуса r ₀ (рис. 9.9).

Рис. 9.9.

Расстояние от источника до центра сферического фронта волны О обозначим символом и от точки О до точки – символом (рис. 9.10).

Рис. 9.10.

Найдем амплитуду волн в точке Р, используя принцип Гюйгенса-Френеля. Разделим волновую поверхность АВ на зоны, колебания от которых приходят со сдвигом оптической длины пути на , а фазы - на p.

Пусть r₀ << a, r₀ <<b, тогда расстояние от источника до преграды можно считать равным a и расстояние от точки Р до преграды равным b (рис. 9.10).

Найдем высоту шарового сегмента и радиус m – ой зоны (рис. 9.11):

,

.

Рис. 9.11.

При малых m можно пренебречь последним слагаемым:

. (9.14)

Площадь сферического сегмента S = 2prh, следовательно, площадь поверхности m – ой зоны:

.

, отсюда радиус m – ой зоны

. (9.15)

Число открытых зон Френеля определяется из условия, что максимальный радиус равен .

.

Амплитуда в точке Р:

.

Перед A_m стоит знак «+», если m – нечетное и знак «-», если m – четное.

.

Примем приближенно:

, , …

Отсюда следует:

.

При малых m амплитуда A_m мало отличается от А₁, поэтому А» А₁ при нечетных m, и А» 0 при четных m.

Амплитуда, создаваемая в некоторой точке Р всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной центральной зоной.

Таким образом, преграда с отверстием, открывающая небольшое нечетное число зон, не только не ослабляет освещение, но и приводит к увеличению интенсивности света.

9.6. Дифракция на пространственной решетке

Рентгеновские лучи представляют собой электромагнитные волны с длиной волны l порядка 5×10^-9 ¸ 10^-11м. Для обнаружения дифракции рентгеновских волн необходимо, чтобы размеры щелей и преград, образующих правильную решетку на пути волн, были не слишком велики по сравнению с l. При d >> l дифракция не наблюдается. Такие решетки нельзя изготовить, но в природе имеются естественные дифракционные решетки – кристаллы. В кристаллах рассеивающим элементом является атом или молекула, они образуют трехмерную решетку. Русский ученый Ю.В. Вульф и английские физики У.Г. и У.Л. Брегги предложили следующий простой способ расчета дифракционной картины от кристаллической решетки. Если на кристалл падает плоская волна, то атомы, лежащие в плоскости атомного слоя, будут отражать волну по обычному закону отражения. Отразившись от различных атомных слоев, плоские вторичные волны будут интерферировать так же, как и волны от щелей дифракционной решетки (рис. 9.12).

Рис. 9.12.

Поиск по сайту: