Опыт Юнга

Для наблюдения интерференции света Юнг разделил волну от источника N, поместив на пути волны экран Э₁ с двумя узкими отверстиями в виде щелей (рис 8.2).

Источники света N₁ и N₂ - когерентные. Свет от источников N₁ и N₂ приходит в точку P на экране Э₂. Расстояние от источников до экрана Э₂ обозначим l, а расстояние между источниками N₁ и N₂ обозначим d.

Координату точки P на оси x будем отсчитывать от точки O, расположенной симметрично относительно источников N₁ и N₂ на экране Э₂.

Начальные фазы волн, вышедших из источников N₁ и N₂, будем считать одинаковыми.

Найдем оптическую разность хода волн, пришедших в точку Р.

,

,

,

.

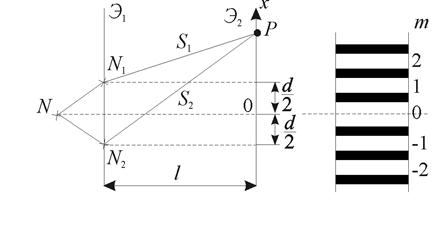
Рис. 8.2.

Примем, что при d << l:

,

отсюда:

. (8.8)

Умножим S₂ - S₁ на показатель преломления среды n, получим оптическую разность хода:

. (8.9)

Найдем координаты максимума и минимума интенсивности. Из условия максимума:

, (m = 0,1,2,…)

находим:

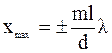, (8.10)

здесь m – порядок максимума;

- длина волны в среде.

Аналогично находим координаты минимума интенсивности:

. (8.11)

На экране Э₂ мы видим интерференционную картину в виде чередующихся светлых и темных полос. Центральная светлая полоса на интерференционной картине называется нулевой, т.к. разность хода равна нулю для всех длин волн. Шириной интерференционной полосы называется расстояние между соседними максимумами или минимумами:

. (8.12)

8.3. Многолучевая интерференция

Рассмотрим случай, когда интерферирует много световых лучей. В данную точку экрана приходит N лучей одинаковой интенсивности, но фаза каждого следующего луча смещена относительно фазы предыдущего на величину d.

Представим гармонические функции в виде экспоненциальных функций или где 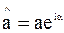- комплексная амплитуда:

При выполнении над комплексными функциями операций сложения, дифференцирования и интегрирования, вещественная часть результата совпадает с результатом выполнения тех же операций над вещественными частями функций:

.

,

.

После произведения вычислений, следует взять вещественную часть полученного результата.

Представим колебания в виде экспонент:

.

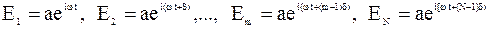Результирующее колебание имеет вид:

.

Полученное выражение представляет собой сумму членов геометрической прогрессии.

Поскольку интенсивность пропорциональна квадрату амплитуды

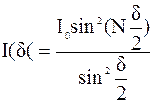. (8.13)

При 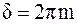возникает неопределенность вида 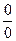. Раскрывая эту неопределенность по правилу Лопиталя, находим:

.

В точки, для которых 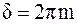, все колебания приходят в одинаковой фазе. Результирующая амплитуда в этих точках оказывается в N раз больше амплитуды отдельного колебания, а интенсивность в N² раз больше. Места, в которых наблюдается интенсивность, определяемая этим соотношением, называются главными максимумами, а число m – порядком главного максимума.

Рис. 8.3. График функции 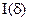для N = 8. На графике для сравнения показан график интенсивности для N = 2, что соответствует двухлучевой интерференции.

8.4. Интерференция света в тонких пленках

Радужные цвета на поверхности воды, покрытой пленкой бензина или цвета побежалости, возникающие на поверхности металла при образовании оксидной пленки, являются примерами интерференции света.

При падении световой волны на тонкую прозрачную пленку или пластинку толщиной b происходит отражение от обеих поверхностей пластинки, при этом возникают две световые волны, которые могут интерферировать.

Рис. 8.4. Интерференция при отражении от тонких пленок или пластинок.

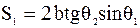- длина отрезка BC;

- сумма длин отрезков AO и OC.

Отсюда следует:

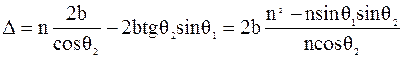. (8.14)

Проведем в (8.13) преобразование: :

.

Найдем разность хода и разность фаз, учитывая, что при отражении света от границы раздела оптически менее плотной с оптически более плотной средой разность хода увеличивается на , а фаза волны увеличивается на p:

, (8.15)

.

Условие максимума при интерференции будет выполняться при определенной длине волны для заданного угла падения q₁, при этом поверхность окрасится одним цветом. При изменении угла падения, цвет будет изменяться. Если пластинка имеет переменную ширину, то окраска меняется на разных участках. Толщину пленки можно определить, измеряя угол падения света и длину отраженной волны.

Поиск по сайту: