Закон Ампера

Сила, действующая на прямолинейный проводник с током I, находящимся в однородном магнитном поле, прямо пропорциональна току I, длине проводника l, магнитной индукции B и синусу угла между направлением тока в проводнике и вектором B:

. (1.7)

В векторной форме закон Ампера:

. (1.8)

На элемент тока , расположенный под углом к линиям магнитной индукции B, действует элементарная сила:

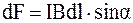, (1.9)

или в векторной форме:

. (1.10)

Результирующая сила, действующая на проводник произвольной формы, находящийся в неоднородном поле магнитном поле:

.

Ампер установил правило левой руки, согласно которому определяется направление вектора силы F.

Если направить указательный палец левой руки по полю, а средний по направлению тока, то отогнутый большой палец укажет направление силы, действующей на ток (рис. 1.10).

Рис. 1.10.

ГЛАВА 2. Магнитное поле движущегося заряда и проводников с токами в вакууме

2.1. Магнитное поле равномерно движущегося заряда

2.2. Закон Био-Савара-Лапласа

2.3. Магнитная индукция поля прямолинейного проводника с током

2.4. Магнитная индукция на оси кругового проводника с током

2.1. Магнитное поле движущегося заряда

Как нам известно, напряженность E является силовой характеристикой электрического поля:

, (2.1)

где F - сила, действующая на пробный заряд q', помещенный в некоторую точку поля.

Магнитная индукция B является силовой характеристикой поля. Сила, действующая на движущийся заряд, называется силой Лоренца:

. (2.2)

Поскольку в природе не обнаружены магнитные заряды, то неправомерно использовать аналогию с электрическим полем, чтобы найти выражение для силы взаимодействия магнитных зарядов.

Можно предположить, что магнитная индукция заряда q, движущегося со скоростью v, пропорциональна величине заряда и скорости. Поскольку вектор B направлен перпендикулярно скорости v, то в формуле должен быть еще один вектор. Причем в формуле должно присутствовать векторное произведение, чтобы в результате получить векторную величину B. В качестве этого вектора можно взять радиус-вектор заряда r, проведенный из точки, где находится заряд, в некоторую точку поля А (рис. 2.1).

Магнитная индукция не может возрастать пропорционально расстоянию от заряда. Если предположить, что магнитное поле изменяется пропорционально , то магнитную индукцию можно записать в виде:

, (2.3)

где k - коэффициент пропорциональности, ;

- единичный вектор, направленный вдоль вектора r.

Вектор магнитной индукции B движущегося заряда перпендикулярен к векторам v и r и обратно пропорционален квадрату расстояния от заряда до данной точки поля. Справедливость полученной формулы подтверждена экспериментально.

Электрическое поле движущегося заряда определяется формулой:

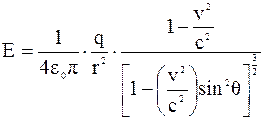, (2.4)

где - угол между вектором скорости v и радиус-вектором r; с – скорость света: .

Если v << c, то электрическое поле движущегося заряда не отличается от электростатического поля неподвижного заряда.

Напряженность магнитного поля движущегося заряда связана с напряженностью электрического поля соотношением:

.

2.2. Закон Био-Савара-Лапласа

Магнитное поле в точке А, создаваемое элементом тока , направлено по касательной к силовой линии, проходящей через данную точку и определяется правилом правого винта (рис. 2.2).

Закон Био-Савара-Лапласа:

Магнитная индукция d B, создаваемая элементом тока на расстоянии r от него, обратно пропорциональна квадрату расстояния и прямо пропорциональна произведению элемента тока на синус угла между векторами и r.

. (2.5)

В скалярной форме:

, (2.6)

где - магнитная проницаемость среды.

Вектор магнитной индукции d B перпендикулярен к вектору элемента тока и радиус-вектору r.

Рис. 2.2.

Био Жан Батист (1774 -1862) - французский физик, родился в Париже, окончил Политехническую школу. В 1820 г. вместе с Ф. Саваром открыл закон, определяющий напряженность магнитного поля прямого тока (закон Био-Савара). Исследовал поляризационные свойства многих веществ. Открыл закон вращения плоскости поляризации света (закон Био) и установил существование право- и левовращающих веществ.

2.3. Магнитная индукция поля прямолинейного проводника с током

Прямолинейным называется ток, текущий по тонкому прямому проводу бесконечной длины. Найдем магнитную индукцию элемента тока в точке А.

Проведем радиус-вектор r из основания элемента тока (точка О) и вектор из вершины элемента тока (точка Q) в точку А (рис. 2.3). Опустим перпендикуляр из точки Q на прямую OА. Обозначим - угол между векторами r и . Используем следующие соотношения:

,

где а - кратчайшее расстояние от прямолинейного проводника до точки А. Найдем магнитную индукцию элемента тока как функцию от угла a:

(2.7)

Рис. 2.3.

Поскольку рассматривается магнитное поле бесконечного проводника, то угол a изменяется от 0 до p. Найдем магнитную индукцию бесконечного прямолинейного проводника с током:

. (2.8)

Найдем теперь магнитное поле, создаваемое отрезком проводника с током в точке А находящейся на расстоянии а от проводника. Построим вектор элемента тока в начале и в конце отрезка проводника и проведем из этих точек радиус-векторы и (рис. 2.4). Обозначим углы между элементами тока и радиус-векторами через a₁ и a₂. Проинтегрируем выражение (2.7) по углу a и найдем магнитную индукцию отрезка проводника с током:

Рис. 2.4.

2.4. Магнитная индукция на оси кругового проводника с током

Рис. 2.5.

Построим элемент тока в верхней части кругового проводника с током. Проведем радиус-вектор r из основания элемента тока в точку А (рис. 2.5). Вектор d B перпендикулярен к векторам и r и находится в плоскости рисунка. Обозначим проекцию вектора d B на ось кругового проводника и перпендикулярную к ней проекцию . При интегрировании по всем элементам тока перпендикулярные компоненты поля взаимно сократятся.

Вектор магнитной индукции кругового проводника с током будет направлен вдоль оси, его величина равна:

, (2.9)

где х - расстояние от точки А до центра кругового проводника;

R - радиус витка;

q - угол между вектором d B и осью кругового проводника.

Применяя закон Био-Савара-Лапласа для поля элемента тока (2.7), находим магнитную индукцию на оси кругового проводника:

(2.10)

Магнитную индукцию в центре кругового проводника с током найдем, положив x = 0:

. (2.11)

Получим это выражение более простым путем. Возьмем круговой проводник с током. Построим вектор элемента тока , направленный по касательной к проводнику (рис. 2.6). Проведем радиус-вектор R из основания элемента тока в центр кругового проводника. Согласно правилу правого винта, поле элемента тока в центре кругового проводника направлено перпендикулярно к его плоскости. Угол a между вектором и вектором R составляет , т.к. касательная перпендикулярна к радиус-вектору R.

Рис. 2.6.

Найдем поле кругового проводника по закону Био-Савара-Лапласа:

.

Контрольные вопросы:

1. Магнитное поле движущегося заряда.

2. Магнитная индукция элемента тока.

3. Правило правого винта.

4. Закон Ампера. Правило левой руки.

5. Взаимодействие параллельных проводников с токами.

6. Применение закона Био-Савара-Лапласа для расчета магнитного поля проводника с током и отрезка проводника с током.

7. Применение закона Био-Савара-Лапласа для расчета магнитного поля на оси и в центре кругового проводника с током.

ГЛАВА 3. Закон полного тока для магнитного поля в вакууме

3.1. Теорема о циркуляции. Магнитное поле соленоида с током

3.2. Магнитный поток. Теорема Остроградского-Гаусса для вектора магнитной индукции

3.3. Магнитный момент кругового тока

3.4. Контур с током в магнитном поле

3.5. Работа перемещения проводника с током в постоянном магнитном поле

3.1. Теорема о циркуляции. Магнитное поле соленоида с током

Циркуляцией вектора магнитной индукции B по замкнутому контуру называется интеграл . Под знаком интеграла стоит скалярное произведение вектора B и вектора элемента длины контура .

Пусть вначале имеется один прямолинейный проводник с током I, направленным перпендикулярно чертежу (рис. 3.1). Проведем вокруг него в плоскости чертежа замкнутый контур радиусом а:

Рис. 3.1.

Выберем в этом контуре элемент длиной d l и направим по касательной к контуру по направлению обхода контура. Найдем скалярное произведение векторов B и d l:

. (3.1)

где - проекция вектора d l на направление вектора B;

а - расстояние от проводника с током до элемента dl.

При обходе по контуру, охватывающему ток:

.

Пусть контур охватывает один проводник с током, тогда циркуляция вектора B:

. (3.2)

Если контур охватывает n проводников с токами, то согласно принципу суперпозиции:

. (3.3)

Поиск по сайту: